Newsletter contents...

Background

The statistic S_c (Lawrence & Colman, 1993) measures the geometric surface complementarity of protein-protein interfaces. S_c depends both on the relative shape of the surfaces with respect to each other and on the extent to which the interaction brings individual elements of the opposing surfaces into proximity. The first dependence is via the use of normal products, and the second dependence is via an inverse exponential dependence on the distance of separation. The original SC software was distributed as a developmental version. The author's current version has now been released in CCP4 and is completely revised. It is considerably faster and easier to use than the developmental version.

In the original article the authors computed S_c for a number of different types of protein / protein interfaces and concluded that protein antibody / protein antigen interfaces appeared on average less complementary than both protein subunit / protein subunit interfaces and protein / protein inhibitor interfaces. This result was rationalized on the basis that the evolution of an antibody-antigen interface occurs in a different fashion to that of a protein subunit / protein subunit interface or a protein / protein inhibitor interface. It also appeared consistent with the observation that antigen binding sites on antibodies contain on average a higher percentage of aromatic residues (Padlan, 1990) than other interfaces - these residues having fewer conformational degrees of freedom than smaller hydrophobic or polar residues and their prevalence may well be expected to lead to less intimate packing. S_c has also been used to examine the shape complementarity of a T cell receptor in complex with a self peptide bound to a class I MHC molecule (Garcia et al., 1998; Ysern et al., 1998). The shape complementarity S_c was yet lower here than the average for protein antibody / protein antigen interfaces, presumably consistent with the need for a relatively low affinity interaction between the T-cell receptor and the peptide-MHC complex. More recently, higher S_c values have been reported for a T-cell receptor in complex with a foreign peptide bound to a Class II MHC molecule (Reinherz et al., 1999).

Definition of S_c

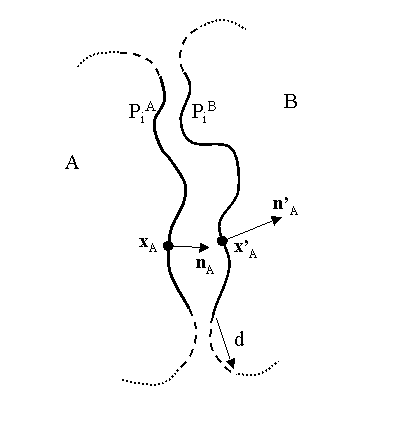
Consider two interacting molecules A and B and their molecular surfaces (Figure 1).

For each molecule we compute that portion of the molecular surface that is buried from the solvent via the interaction with the other molecule - these portions are termed P^A and P^B respectively. A peripheral band is then removed from each of these buried surfaces P^A and P^B by excluding that area of each that is within a distance d of the solvent-exposed portion of the respective molecular surface. The resultant subset of each buried surface is termed P_i^A and P_i^B respectively, where the subscript i denotes "interior". In the above Figure, accessible surface is shown dotted, peripheral surface is shown dashed and interior surface as unbroken line.

For each point x_A in P^A we find its nearest neighbour x'_A on P_i^B. Let n_A be the outwardly-oriented surface normal at x_A and n'_A be the inwardly-oriented surface normal at x'_A. Define the scalar function

S^A->B(x_A) = (n_A. n'_A) exp[-w (|x_A-x'_A|)²]

on the surface P_i^A, where w is a scalar weight.

Likewise by considering all points x_B on surface P_i^B we may define

S^B->A(x_B) = (n_B. n'_B) exp[-w (|x_B-x'_B|)²]

where x'_B is the nearest point to x_B on P^A, n_B the outwardly-oriented normal at x_B and n'_B the inwardly-oriented normal at x'_B.

S_c is then defined as

S_c = ({S^A->B}+{S^B->A}) / 2

where braces denote the median of the distribution of S^A->B(x_A) and S^B->A(x_B) values over P_i^A and P_i^B respectively. Use of the median reduces the dependence of S_c on points that are outliers in the respective distributions.

Numeric calculation of S_c can be achieved via approximating the buried surface surfaces as uniformly distributed sets of points ("dots") sampled in the fashion outlined by (Connolly, 1983). In the standard calculation of S_c (Lawrence & Colman, 1993), d = 1.5 Å, w = 0.5 Å^-2 and the surface sampling density is 15 dots / Å^-2.

Cross comparison of S_c values

As is clear from the definition above, S_c depends not only upon the atomic coordinates, but also upon a set of parameters, and hence any published value for S_c should state the values used for these parameters. The impact of these various values upon S_c are as follows:

1. Atomic coordinates

   The atomic coordinates underlie the definition of the protein interface. These coordinates have an error associated with them and the reliability of S_c will consequently be lower for less well-determined structures. However, (Lawrence & Colman, 1993) argue that coordinate error, given its relatively random nature, may not impact greatly on the value of S_c.

   The inclusion of solvent molecules within the interface needs special consideration. (Lawrence & Colman, 1993) suggest performing two calculations of S_c – first with the solvent associated with one molecule and then with the other, and simply taking the average. In other circumstances it may be more appropriate to omit the solvent altogether.

2. Probe and atomic radii

   These radii define the molecular surface and altering them will alter S_c. However, a change in atomic radius at a given site on the interface would not be anticipated to alter substantially the normal product of juxtaposed surface elements, its effect would be through the distance exponential.

3. Width d of excluded interface periphery

   The periphery of the buried interface is excluded from consideration in S_c for the reasons outlined above. Decreasing the width of the excluded band will decrease S_c via the inclusion of intrinsically non-complementary surface.

4. Distance weighting factor w

   The exponential distance weighting factor w acts as a scale factor for the "fit" of the surfaces. Altering this parameter should not affect S_c for highly complementarity surfaces, but will have a significant effect on S_c for more poorly fitting surfaces.

5. Surface point density

   Under-sampling the molecular surfaces should be avoided as this will have a marked impact on S_c. Test calculations show that the computation is stable at a dot density of around 15 / Ų.

The CCP4 version SC is distributed with the same set of radii and default parameters that accompanied the original software obtained from the author and which were used in the calculations cited in (Lawrence & Colman, 1993). These values should be used for all calculations if cross-comparison is to be made with already-published literature values of S_c.

Major improvements contained in the CCP4 version of SC

A number of major improvements have been made to the SC software:-

1. Surface calculation is now carried out within the program, rather than piping intermediate results to Connolly's MS program in a stand-alone fashion. The program also now incorporates Connolly's new mds subroutine (obtainable from http://www.biohedron.com), which has a faster surface generation algorithm than the original MS.

2. Selection of interface atoms is now done via a distance metric, avoiding the need for the initial low density surface computation.

3. Molecule definition is now handled via a chain/residue/atom name parser.

4. The interface to GRASP (Nicholls, 1993) is now incorporated directly in the program.

5. Graphical output of S^A->B, S^B->A and distance histograms is now provided in CCP4 xloggraph-compatible form.

Conclusions

S_c is established as a useful tool quantifying the geometrical packing of protein interfaces and the new CCP4 version SC should greatly facilitate its use.

Given the large increase in the number of structures available since the original work of (Lawrence & Colman, 1993), it would be appropriate to re-assess the original conclusions regarding the complementarity of antibody-antigen interfaces compared to other forms of protein-protein interfaces, and also to consider extending these calculations to assess the broader range protein protein-receptor complexes that are now available. Such work is in progress in our laboratory (see for example (Epa and Colman, 2001)).

Acknowledgments

I thank my colleague Brian Smith for assistance with coding the new version of SC, Michael Connolly for making available the mds subroutine and Peter Briggs for incorporating CCP4 compatibility into SC.

Connolly, M. L. (1983). Analytical molecular surface calculation. J. Appl. Crystallogr. 16, 548-558.

Epa, V.C. & Colman, P.M. (2001). Shape and Electrostatic Complementarity at Viral Antigen-Antibody Complexes. Curr. Topics. Microbiol. Immunol. (in press).

Garcia, K. C., Degano, M., Pease, L. R., Huang, M., Peterson, P. A., Teyton, L. & Wilson, I. A. (1998). Structural basis of plasticity in T cell receptor recognition of a self peptide-MHC antigen. Science 279, 1166-1172.

Lawrence, M. C. & Colman, P. M. (1993). Shape complementarity at protein/protein interfaces. J. Mol. Biol. 234, 946-950.

Nicholls, A. J. (1993). GRASP: graphical representation and analysis of surface properties. Biophys. J. 64, A116.

Padlan, E. A. (1990). On the nature of antibody combining sites: unusual structural features that may confer on these sites an enhanced capacity for binding ligands. Proteins 7, 112-124.

Reinherz, E. L., Tan, K., Tang, L., Kern, P., Liu, J., Xiong, Y., Hussey, R. E., Smolyar, A., Hare, B., Zhang, R., Joachimiak, A., Chang, H. C., Wagner, G. & Wang, J. (1999). The crystal structure of a T cell receptor in complex with peptide and MHC class II. Science 286, 1913-21.

Ysern, X., Li, H. & Mariuzza, R. A. (1998). Imperfect interfaces. Nature Struct. Biol. 5, 412-414.

Newsletter contents...