1. Introduction

The mosflm package for the integration of macromolecular diffraction data consists of two components, iMosflm (Battye et al., 2011) and ipmosflm (Leslie & Powell, 2007; Leslie, 2006). iMosflm (Fig. 1) is a Tcl/Tk based graphical user interface (GUI) that, via a series of panes, is designed to guide the user through the different steps in integrating a set of diffraction images. It allows inspection of the images and provides graphical feedback on the processing, for example by displaying the predicted reflection positions superposed on the diffraction image and plotting the variation in refined parameters and the standard reflection profiles. It also allows the user to change a large number of parameters that can influence the processing, to provide flexibility when dealing with particularly challenging datasets. iMosflm sends the necessary instructions to the ipmosflm background process that performs all the intensive computation. Information about refined parameters, standard profiles etc are passed from ipmosflm to iMosflm for display in the GUI. Data can be processed with ipmosflm alone by providing the necessary keyword commands, but this requires a much greater familiarity with the program than when using the iMosflm interface.

Both components are being continually developed and this article summarises the more recent developments that are available in the imminent release of ipmosflm version 7.0.9 (matched to iMosflm 1.0.7)

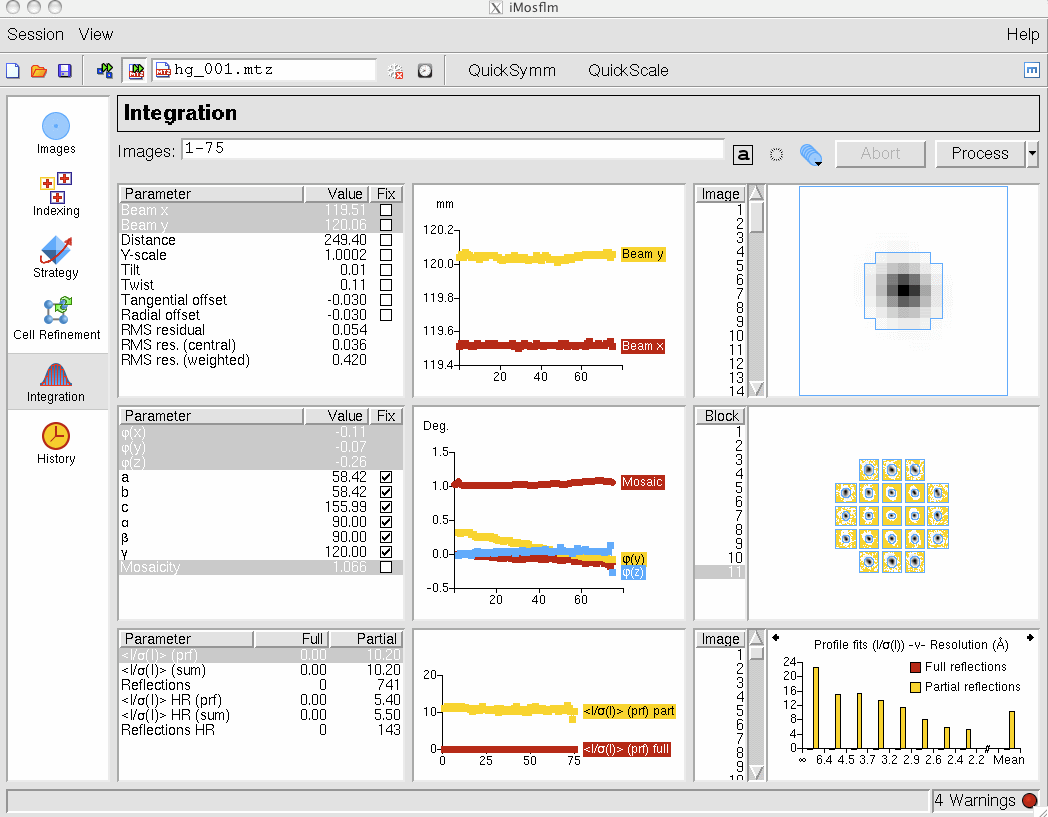
::ccp4:CCP4_meeting_2010:Figures:fig1_new.tiff

Figure 1. The Integration pane of the iMosflm graphical user interface.

2. Dealing with fine sliced, low exposure or weak diffraction images from Pilatus detectors

There were a number of issues that arose when processing Pilatus images collected with very short exposure times and very small oscillation angles, so that a significant number of pixels had values of zero. The refinement of the detector and crystal parameters were also sometimes unstable in such cases. These problems were mainly addressed in a beta release of iMosflm (version 1.0.6)/ipmosflm (version 7.0.8) in July 2011. This was a beta release because the problems were sufficiently serious to merit a new release, but there was insufficient time to carry out the usual full release testing. Further improvements in the processing of fine-sliced data have been made since that beta release.

Visualisation of the images is challenging when the exposure times are very short, with spots tending to vanish in the background noise, making it difficult to assess the quality of the diffraction. No satisfactory solution to this problem has been found yet, so in practice it is advisable to view a zoomed outer region of the image when deciding on the diffraction limit. The predicted pattern can also be difficult to see in such cases as the yellow boxes of the partial reflections become barely visible. There is now the option to change the colour of the boxes for the four different classes of reflection (full, partial, overlapped, too wide in phi) to overcome this problem (Fig. 2).

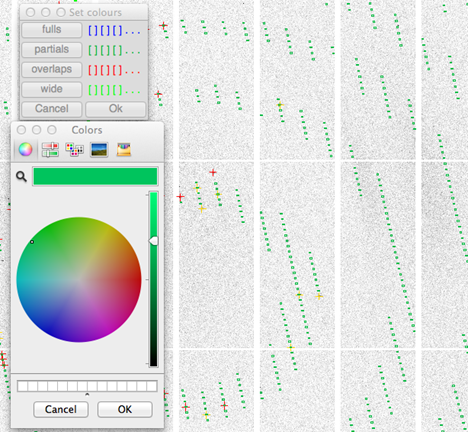
ColourPredictionsMac.tiff

Figure 2. Colours can be chosen for the prediction boxes of each class of reflection.

Another issue arose when attempting to index diffraction patterns obtained from in situ samples at the Diamond Light Source. In these cases, the very small size and very low mosaicity of the crystals can result in diffraction spots that are only 1-2 pixels across. Changes to the spot finding algorithms were required to prevent these very small spots from being rejected, but once these were implemented indexing became straightforward.

In general, 3D profile fitting can offer advantages with very small oscillation angles (so-called fine phi slicing), but tests have shown that the 2D integration in mosflm provides excellent data quality even on challenging datasets (high mosaicity and weak diffraction) with oscillation angles as small as 0.1 degrees.

3. Avoiding corruption of the standard profiles by ice spots or “hot pixels”

The “standard profiles” used to evaluate the profile-fitted intensity are derived by the simple addition of all spots in a local region of the detector. As a result, it is possible for ice spots, zingers or single “hot” pixels (pixels that have an approximately constant value (that can be very large) on all images) to corrupt the standard profiles, especially if the diffraction spots are relatively weak.

An example of corruption by ice rings is shown in Fig. 3. To prevent this effect, two stages of filtering are applied when forming the standard profiles. Firstly, reflections that lie within a narrow resolution shell centred on the d-spacings for ice are omitted. The required width of the shell will depend on the strength of the ice diffraction and can be changed in iMosflm in the Processing Options. Secondly, in order to remove the influence of zingers or hot pixels, a small number of reflections that have the largest pixel intensity values are also excluded. This number can also be controlled, but defaults to 5%. As shown in Fig. 3, these steps are very effective in removing unwanted spots from the profiles.

corrupt_profiles.tiff

Figure 3. (A) Diffraction pattern showing strong ice rings. (B) Standard profiles without reflection filtering. (C) Standard profiles with reflection filtering.

4. An improved multi-crystal strategy option

The “Strategy” pane in iMosflm provides a straightforward means of calculating a geometrical strategy (ie a phi start and phi end) for cases where the user does not wish to collect a full 180 degree rotation, assuming that the correct Laue group is known. However, although possible in principle, it was not simple to use this option to devise a strategy when data were collected from different crystals in different orientations (without the use of a multi-circle goniostat to allow re-orientation of the crystals).

A new strategy pane has been implemented that greatly simplifies this task (Fig.4). Briefly, the procedure is as follows. One or more reference images are read for the first crystal and indexed in the normal way. In the Strategy pane’s Auto-complete menu, the user specifies how many degrees of data they expect to be able to collect from this crystal, and a start and end phi value for this crystal are calculated. Once these data have been collected, reference images for the second crystal are indexed. On entering the Strategy pane, the segment recommended (and assumed collected) for the first crystal will be displayed graphically. Running the strategy calculation again for the second crystal will then provide a start and end phi for the second crystal that will result in the highest possible completeness for crystals 1 and 2 combined. In Fig. 4, data have already been collected from two crystals (Ade12 and Ade16) and the strategy is being calculated to find the best 20 degree segment for the third crystal, Ade21.

The procedure can be repeated for further crystals. A summary of the recommended start/end phi values for each crystal are displayed at the top of the Strategy pane (Fig. 4) and this information can be saved and restored if it is necessary to exit the program. Furthermore, the phi values for each crystal can be updated graphically by manipulating the sector (wedge) displayed as a chart for the selected crystal. Thus if a particular crystal only provided 10 degrees of data instead of the expected 20 degrees, due to radiation damage, the phi end value can be updated and this revised value will be taken into account in future strategy calculations.

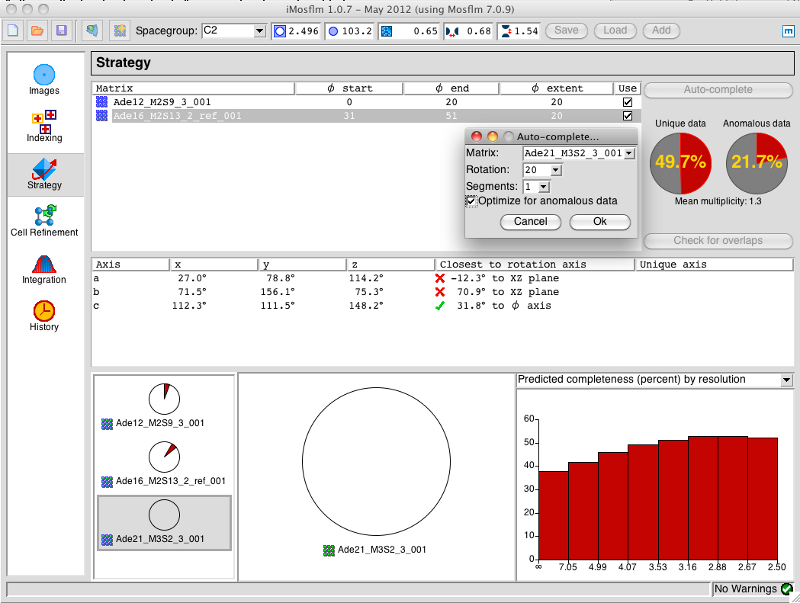
StrategyComplete.tiff

Figure 4. The new Strategy pane that simplifies strategy prediction when using multiple crystals for data collection.

5. The “mosaic blocksize” parameter

The “mosaic blocksize” parameter allows for the effect of very small mosaic blocks or domains on the dimensions of the reciprocal lattice spots and hence the reflecting range of Bragg reflections (Juers et al., 2007; Nave, 1998). In practice, it has the same effect as having a larger mosaic spread at low resolution than at high resolution. The effect of different mosaic blocksizes on the predicted reflections can easily be modelled in iMosflm by changing the default blocksize (100 microns) on the Images pane. As yet there is no procedure to refine this parameter, and the optimum value must be determined by running multiple processing jobs with different values and examining the merging statistics. Using too large a value will result in under-prediction of low-resolution reflections, which in turn can give higher values for Rmerge and the partial bias (FRCBIAS), while using too small a value will result in significant over-prediction at intermediate and higher resolutions, with resulting increases in Rmerge. A systematic investigation of the effect of varying the mosaic blocksize on a dataset from a crystal containing the lanthanide Praseodymium has shown that this parameter can have a significant effect on the anomalous signal at low resolution in addition to the other statistics (Table 1). In this case, a mosaic blocksize of 0.25mm gave the best anomalous correlation coefficients. Lack of time has not allowed a proper investigation of how this would affect ab initio structure determination (in this case the structure was determined by a combination of molecular replacement and SAD phasing), but the improvement in the anomalous correlation coefficient indicates that at least in marginal cases it is worth investigating the effect of optimizing this parameter.

Blocksize mm	Anomalous Correlation Coefficient Overall Low High			Rmerge Overall Low High			FRCBIAS Overall Low High
100	0.421	0.552	0.077	0.168	0.073	0.401	-0.017	-0.039	0.043
10	0.414	0.640	0.074	0.171	0.076	0.402	-0.015	-0.043	0.064
1	0.454	0.684	0.058	0.168	0.072	0.404	-0.003	-0.044	0.087
0.75	0.454	0.660	0.075	0.170	0.071	0.414	0.001	-0.042	0.072
0.5	0.481	0.688	0.056	0.166	0.067	0.407	-0.003	-0.033	0.059
0.25	0.547	0.859	0.120	0.161	0.053	0.411	0.000	-0.013	0.041
0.15	0.445	0.797	0.046	0.183	0.050	0.499	0.001	0.001	0.060
0.1	0.459	0.833	0.030	0.186	0.052	0.439	0.009	0.017	0.052

Table 1. Statistics obtained from AIMLESS using different mosaic blocksizes in mosflm. The mid-bin resolutions for Low and High resolution bins in the Table are 7.16 Å and 3.44 Å.

6. Improved selection of the optimal indexing solution in cases of pseudosymmetry

In cases of pseudosymmetry, for example a monoclinic crystal with a b angle close to 90 degrees, or an orthorhombic crystal with very similar a and b cell dimensions, there can be an ambiguity in selecting the correct indexing solution. Previously the solution highlighted in the Indexing pane of iMosflm was selected based only on the indexing penalty. Careful analysis of a large number of reference images collected as part of the DNA project (Leslie et al., 2002) demonstrated that the rms error (rmsd) in spot positions (s(x,y) in iMosflm) can be used as a reliable indicator of the correct solution. In particular, if the rmsd for a particular solution is more than 1.3 times the rmsd of the triclinic solution, then the true symmetry is probably lower. A combination of the penalty value and the rmsd value are therefore now used to select the most likely indexing solution. At present, this is only implemented when the indexing is carried out from iMosflm, not when ipmosflm is used independently.

7. Mosaicity refinement

The correlation between cell parameters and mosaicity during post-refinement can result in the mosaicity refining to zero if the cell parameters are inaccurate. This problem has been minimized by keeping the mosaicity fixed during the initial cycle of cell refinement, and if there is a large shift in cell parameters the mosaicity is reset to its initial value for the next cycle. These changes have improved the reliability of the refinement, but there are still some circumstances in which the mosaicity can refine to either too large or too small a value, both in cell refinement and integration. This is typically associated with split diffraction spots or a combination of high mosaicity and large cell dimensions that results in adjacent reflections not being fully resolved in phi. In some cases, the only way to deal with this situation is to fix the mosaic spread at an appropriate value (estimated by visually comparing observed and calculated predictions), while in others assigning an appropriate mosaic blocksize can stabilize the mosaicity refinement. The partial bias statistic (FRCBIAS in SCALA or AIMLESS) should always be checked to see if there is evidence that the mosaic spread has been underestimated.

8. Further improvements

A variety of additional enhancements have been made. The most significant is a dramatic improvement in the speed of processing of datasets consisting of more than a few hundred images with iMosflm. Previously the rate of processing dropped dramatically after about 500 images, making the processing of fine sliced data very tedious. The rate of processing is now essentially constant when tested for over 1000 images. This improvement was present in the beta release of July 2011.

Phil Evans’ program AIMLESS, a replacement for SCALA, is now the default when running the Quickscale option in iMosflm (but SCALA can be selected from the Processing Options). The data quality statistics are generally better using AIMLESS and it is typically three times faster than SCALA.

During post-refinement, there is now an option to select how the total intensity of a partially recorded reflection is divided up for use in post-refinement. Previously this was done so that approximately the same intensity was assigned to the two “parts” of the partial (corresponding to a PARTIAL value of 0.5) and this works well with “coarse sliced” data. However, for fine sliced data, the refined mosaicity tends to be too small using this approach, and a PARTIAL value of 0.25 works better, but this leads to unstable behaviour for “coarse sliced” images. Currently the default value depends on the oscillation angle and is set to 0.5 for oscillation angles greater than 0.25 degrees, 0.35 for angles greater than 0.15 degrees and 0.25 for angles less than 0.25 degrees, but can be set manually via the Processing Options.

The algorithm for estimating the mosaic spread has been improved so that it gives a more realistic estimate in cases of very high mosaicity.

Finally, some changes have been made to the estimation of the standard deviations in the intensities. In particular, the contribution of the detector error to the standard deviation (see 5.3 in Leslie, 1999) is still used for the statistics presented in iMosflm and the mosflm logfile, but it is not included in the standard deviations that are written to the output MTZ file. This contribution is now modelled by the SDADD term in SCALA or AIMLESS, which will therefore be systematically larger for data processed with the latest version of mosflm. This change was made because the contribution from this source of error was not properly modelled for partially recorded reflections and is better applied after the partial intensities have been summed. For one dataset with a weak anomalous signal that contained a large fraction of fully recorded reflections, this change made a significant difference to the success rate of the substructure determination.

9. Future developments

Significant progress has been made recently in the task of identifying and indexing multiple lattices and work is in progress to make this available in the iMosflm interface. This will be developed to allow the integration of each lattice separately, taking into account the presence of the other lattices. In the longer term, this will require a change in structure of the existing MTZ file format, to allow multiple indices to be assigned to a single intensity in order to deal with those cases where reflections from two lattices overlap.

A second topic under investigation is to speed up the integration by dividing a dataset into multiple blocks of images and integrating these in parallel, taking advantage of the fact that many machines now have multiple cpus. This has been demonstrated in principle, but two aspects require further work. Firstly, it is necessary for iMosflm to assemble the graphical output from each of the parallel jobs so that this can be presented in the GUI as if the integration were done serially rather than in parallel. Secondly, extensive testing is required to ensure that the separate integration of many blocks of data does not have any adverse effect on data quality.

Finally, we hope to implement a “traffic light” style of representing the many warnings that mosflm can produce, where red would indicate a serious error, amber would mean that the warnings should be checked but are not serious, and green to indicate satisfactory processing. This would be linked to more detailed (and hopefully more understandable) error messages, and some progress has already been made in that respect.

Acknowledgements

We gratefully acknowledge all those who have provided useful feedback on the mosflm package, in particular Phil Evans, Graeme Winter, Olof Svensson and Frank von Delft. This work is supported by the MRC and BBSRC.

This article may be cited freely.

References

Battye, T.G.G., Kontogiannis, L., Johnson, O., Powell, H.R. & Leslie, A.G.W. 2011. iMosflm: a new graphical interface for diffraction image processing with MOSFLM. Acta Cryst. D67, 271-281.

Juers, D.H., Lovelace, J., Bellamy, H.D., Snell, E.H., Matthews, B.W. & Borgstahl, G.E.O. 2007. Changes to crystals of Escherichia coli b-galactosidase during room-temperature/low-temperature cycling and their relation to cryo-annealing. Acta Cryst D63, 1139-1153.

Leslie, A.G.W. 1999. Integration of macromolecular diffraction data. Acta Cryst. D55, 1696-1702

Leslie, A.G.W., Powell, H.R., Winter, G., Svensson, O., Spruce, D., McSweeney, S., Love, D., Kinder, S., Duke, E. and Nave, C. 2002. Automation of the collection and processing of X-ray diffraction data – a generic approach. Acta Cryst. D58, 1924-1928.

Leslie, A.G.W. 2006. The integration of macromolecular diffraction data. Acta Cryst D62, 48-57.

Leslie, A.G.W. & Powell, H.R. 2007. Processing diffraction data with MOSFLM. in Evolving Methods for Macromolecular Crystallography, Read R.J & Sussman, J.L. (eds), Springer Press, 41-51

Nave, C. 1998. A description of imperfections in protein crystals. Acta Cryst D54, 848-853.