Enhanced Structural Alignment with GESAMT

Eugene Krissinel

CCP4, Research Complex at Harwell, Rutherford Appleton Laboratory, Didcot OX11 0FA, UK

Structural alignment of macromolecules has many applications in structure solution and analysis. Common examples include the comparison of models for molecular replacement, identification of stable domains, conformational analysis, comparative analysis of binding sites and protein function prediction.

The CCP4 Software Suite includes several programs for structural alignment and calculation of best structure superposition: LSQKAB [1], POLYPOSE [2] and SUPERPOSE (also known as Secondary Structure Matching, SSM, [3]). In addition, 3D structure alignment and superposition may be calculated with MOLREP, a program for molecular replacement [4]. These programs are not functionally equivalent to each other. E.g., LSQKAB is extremely fast and efficient but needs a manual input of matching atom pairs. POLYPOSE performs multiple alignment of a large number of structures but assumes them to be of the same length, with one-to-one correspondence between their atoms. The actual structure alignment in CCP4 (i.e. automatic computation of equivalent atom pairs) is done by SSM and MOLREP. SSM was recognized as the fastest and yet a top-quality application in the field [5]. This algorithm was designed primarily for fast searches in structural databases at the European Bioinformatics Institute (EBI), for which certain limitations were adopted. For example, SSM is applicable only to structures with at least several secondary structure elements. In addition, SSM may underperform on fragmented chains and, in certain cases, it prunes search trees if favourable for speed. MOLREP is free from SSM limitations, however, structural alignment is by far not the main option for this application, and comes as a by-product of a more general task. As a result, structural alignment in MOLREP is slow for interactive applications and database searches.

Development of GESAMT (General Efficient Structural Alignment of Macromolecular Targets) was motivated as an attempt to complement the Suite with a structural aligner, which would be comparable to SSM in performance and quality but free of SSM’s limitations. In particular, applicability to incomplete structures, which do not allow for a reliable identification of secondary structure elements and may be highly fragmented, was an essential requirement.

In its essence, GESAMT may be found similar to other structural alignment algorithms, such as Combinatorial Extension (CE) [6]. At first stage, the given chain-wise structures S₁ and S₂ are represented as sequences of short overlapping fragments. Next, GESAMT superposes all fragments of S2 onto fragments of S1, and clusters the results in superposition matrix space. Finally, the largest clusters are refined and extended using iterative dynamic programming along the lines described by Gerstein and Levitt [7].

Two major points make GESAMT different from similar techniques. Firstly, clustering of short fragments is done using a global (structure-based), rather than a local (fragment-based) distance measure in superposition matrix space. Global assessment is considerably more time consuming than the local one. However, it results in a rather aggressive removal of unsuitable fragment superpositions at early stages, which results in a dramatic decrease of the total number of primary acts of assessment. Overall, it was found that using an expensive, but aggressive assessment technique results in a surprisingly efficient “quenching” of combinatorial explosion, which other methods (such as CE) tackle with an empiric set of rules for the pruning of the search space.

The second new feature, implemented in GESAMT, is using SSM’s Q-score:

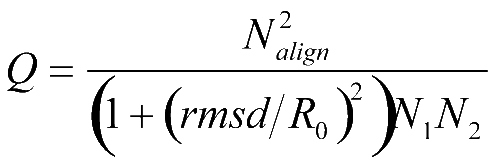
as a target function for the iterative dynamic programming refinement (N_align stands for the number of aligned residues, N_1/2 is number of residues in structures S_1/2, rmsd is the r.m.s.d. calculated between aligned residues at best structure superposition, and R₀ is an empiric parameter for balancing alignment length and r.m.s.d.). Over many years of experience with SSM algorithm, the Q-score was confirmed to be superior to r.m.s.d. and simple distance cut-off scores. However, the Q-score cannot be represented as a sum of effects from the alignment of particular pairs of residues, therefore it cannot be used “as-is” in a dynamic programming algorithm. Therefore, a special procedure was developed, which uses a local linearization of Q-score and converges to solution in a self-consistent manner.

Full details of the GESAMT algorithm will be published elsewhere. Below, we briefly discuss some of its main features. We give them in comparison with SSM, which is a legitimate approach here since both algorithms use the Q-score as a target function in order to identify suitable alignments.

Figure 1 presents Coverage vs. Error [8] plots for Gesamt and SSM. As may be seen, Gesamt provides better identification of similar and dissimilar structures, using SCOP’s definition. This difference is notable on the level of SCOP families at higher coverages, and holds true on fold and class levels at all coverages (sensitivities), where GESAMT gives 3 to 10 times less errors than SSM. Considerable enhancement of structure recognition power makes GESAMT a “must have” alternative to SSM (and possibly other aligners) in structural bioinformatics applications.

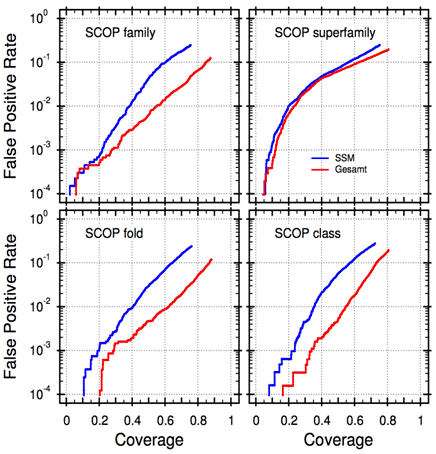
Figure 1. Sensitivity and specificity analysis for GESAMT and SSM (Coverage vs. Error [8]). The FATCAT benchmark set [9], comprising 15002 pairs of structures belonging to similar and dissimilar SCOP domains, was used to generate the curves. Neither SSM nor GESAMT were trained on this benchmark set.

Curiously, GESAMT does not offer a significant improvement of the error rate in case of SCOP superfamilies, where it is limited to a factor of 2 at selected coverages. Here, both SSM and GESAMT reach the highest level of errors comparing to other SCOP categories. The reason for these results remains unclear. In this respect, note that SCOP superfamilies are defined by a probable common evolutionary origin. The results may suggest that SCOP classification of superfamilies is less perfect than that of other categories. Other reasons may equally play a role such as the particular composition of the benchmark set, or indeed there could be something “special” with SSM and GESAMT algorithms, however, the latter was not confirmed by the performed investigations.

Figure 2 presents a comparative analysis of SSM and GESAMT. In the first three panels of Fig. 2, each dot represents a pair of alignments performed by SSM and GESAMT for the same protein pair. The resulting Q-scores and CPU times are used as the dot coordinates.

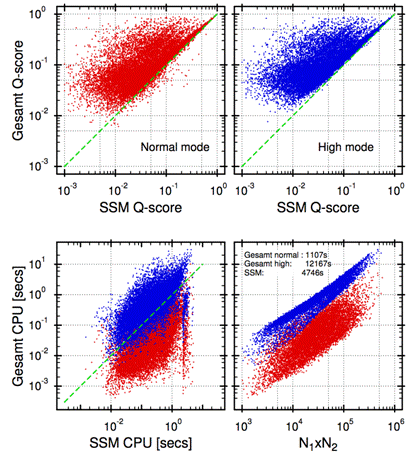
Figure 2. Comparative study of SSM and GESAMT performance on the same benchmark set as the one used in Fig. 1. Red dots correspond to GESAMT running in “Normal” mode, with parameters chosen for the optimal balance of speed and quality (as measured by Q-score). Blue dots correspond to GESAMT in “High” mode, where maximum quality is reached. Figures in low-right panel indicate gross timings (CPU clocks) for the algorithms to process all alignments in the benchmark set.

As any other algorithm of its kind, GESAMT has a few semi-empiric parameters that control the extensiveness of search in alignment field, and ultimately balance the achieved quality (as measured by Q-score) and computation time. For simplicity, these parameters have been combined in two sets, called “Normal” and “High” mode. In “Normal” mode, a reasonable balance between quality and speed is negotiated, while in “High” mode, quality considerations are ultimately preferred.

As seen from the top two panels in Fig. 2, GESAMT reaches considerably higher scores than SSM in most cases. This means GESAMT’s alignments are longer at lower rmsd. Yet, some 5% of total alignments produced by GESAMT in “Normal” mode are lower than those achieved by SSM (cf. top-left panel in Fig. 2). These poorer alignments are attributed to the particular set of GESAMT’s parameters, which allow some trade-in of quality for speed in “Normal” mode. As seen from the top-right panel in Fig. 2, these alignments improve greatly in “High” mode, where the quality of GESAMT’s alignments is at worst equal to that of SSM.

The lower-left panel in Fig. 2 represents a direct comparison of GESAMT and SSM speed on the same benchmark set. As seen from the Figure, GESAMT is most often faster than SSM in “Normal mode” and most often slower than SSM in “High” mode. The timings in the lower-right panel suggest that, on average, SSM takes 0.3 secs per alignment, with “Normal mode” GESAMT 4.3 times faster, and “High mode” GESAMT 2.5 times slower than that. These results indicate that a marginal quality decrease in “Normal” mode is accompanied by a 10-time gain in speed. It is also worth noting here, that this test is not truly indicative in respect to SSM speed. SSM was designed for mass-screening large databases, and allows for efficient precompilation of structural data. With this precompilation in force, SSM’s speed is significantly (20-30 times) faster than indicated in Fig. 2. This particular feature of the SSM algorithm cannot be used in pairwise comparison and is not engaged in CCP4’s SUPERPOSE. However, precompilation of structural data is an essential feature of the SSM web-server running at European Bioinformatics Institute (EBI) [10].

The lower-right panel in Fig. 2 presents complexity analysis for GESAMT. Theoretically, GESAMT’s complexity is estimated as O(N₁xN₂). Linear correlation between measured CPU time and the product of chain lengths is seen rather clearly in “High” mode, while “Normal” mode shows a higher extent of variation from the estimate. This is explained by the earlier mentioned fact that in “Normal” mode, GESAMT exercises greater liberty in pruning the search tree, subject to particular situation and structural features, which often results in better than theoretical complexity.

On the user side, GESAMT mimics SUPERPOSE, which means that it takes the same input and generates the same output. This was done intentionally in order to make switchover from SUPERPOSE to GESAMT as painless as possible for users and related applications.

This article must not be used as a reference for the GESAMT algorithm, and no materials/data from this communication can be used for benchmarking or any comparative studies, or referenced to, unless explicit permission is obtained from the author.

References

[1]     Kabsch, W. (1976) Acta. Cryst. A32 922-923

[2]     Diamond, R. (1992) Protein Sci. 1 1279-1287

[3]     Krissinel, E., and Henrick, K. (2004) Acta Cryst. D60 2256-2268

[4]     Vagin, A., and Teplyakov, A. (1997) J. Appl. Cryst. 30 1022-1025

[5]     Kolodny, R., Koehl, P., and Levitt, M. (2005) J. Mol. Biol. 346 1173-1188

[6]     Shindyalov, I.N., and Bourne, P.E. (1998) Prot. Enginrg. 11(9) 739-747

[7]     Gerstein, M. and Levitt, M. (1996) Using iterative dynamic programming to obtain accurate pairwise and multiple alignments of protein structures. Proc. the 4th International Conference on Intelligent Systems for Molecular Biology, Menlo Park, Calif.: AAAI Press, 59-67

[8]     Brenner S. E., Chotia C. and Hubbard T. J. P. (1998) PNAS 95, 6073-6078

[9]     Ye Y. and Godzik A. (2003) Bioinformatics 19 Suppl 2 II246-II255

[10]   http://www.ebi.ac.uk/pdbe/ssm .