BioCrystallographica,
a package for doing Crystallography with Mathematica
Nicolas Ambert*, Julien Vanwinsberghe*, Philippe
Dumas.
Equipe de Cristallographie
UPR9002 du CNRS conventionnée avec l’ULP
IBMC, 15 rue René Descartes 67084 Strasbourg cedex FRANCE
* N.A & J.V
contributed equally to this work
Corresponding
author: P. Dumas
e-mail:
p.dumas@ibmc.u-strasbg.fr
Abstract
We have made a package for doing
macromolecular crystallography with the software Mathematica from
Wolfram Research. This package contains in its present state all necessary
functions for handling files commonly used and performing all basic
calculations required in daily work. Our goal was obviously not to offer a
stand-alone alternative to well known (and huge) crystallographic packages like
CCP4 or CNS, but to open the way for using a programming language with very
rich symbolic capabilities. To take benefit of existing softwares, we have made
possible to call various CCP4 routines from within the package and to get the
results immediately available in the package environment. Such possibilities
could be easily extended to CNS, or other packages. In its present state, BioCrystallographica
is not really intended for a common usage, but rather to allow those involved
in the field to analyze their results and develop new methods. The Mathematica programming language, as other languages of
that kind, requires a significant practice before being used efficiently,
particularly for abandoning procedural programming methods in favor of functional
ones. This investment, however, is worth the effort in view of the extreme
density of the code and of the depth of the questions that can be addressed.
1. Introduction
There now exists a large number of
crystallographic softwares, most often organized in more or less general
packages. CCP4 (CCP4, 1994) and CNS (Brünger et al.,
1998) are particularly well known examples. Having a look to Jean
Cavarelli’s web site in
2. Essential features and
working environment of Mathematica
Mathematica is organized in two parts: the
so-called ‘front-end’ corresponding to the program-user interface, and the
‘kernel’ receiving the commands from the front-end, doing the calculations and
returning the result to the front-end. Although it is still possible to
interact directly with the kernel in an ‘old-fashioned’ way (i.e. at the
command-line level, e.g. in a unix window), it is obviously much more efficient
and user-friendly to do so through the front-end. This allows to obtain
directly graphical results immediately after the corresponding lines of code,
and also to interact very efficiently with an exhaustive on-line help. The
front-end interface is organized by the user into individual cells that
represent a logical unit of code. This organization is flexible because it may
be modified at will. The input code is interpreted cell by cell if desired,
which also provides a high degree of flexibility during development.
It should be realized that the
essential characteristics of a software like Mathematica resides in its
symbolic capabilities. Therefore, it differs from softwares devoted to
numerical calculations by the fact that, by default, it does not assume that a
general symbol has a precise meaning. For example, defining a simple function
like
without mentioning
anything about the parameters a, b, c and the variable x lets
open the possibility that these may correspond to usual real numbers (with
finite machine precision), to numbers corresponding to symbols with infinite
precision (e.g. p
), to complex numbers, to matrices, or even to
yet undefined symbols that will allow such algebraic calculation. Obviously,
such a burden may have a price in terms of speed, but may also yield results
unattainable with classical ‘purely numerical’ softwares. However, when
restricting the input data to numbers with finite precision, the calculations
become comparable in execution time to that obtained with more specialized
softwares. For example, obtaining the eigen values of a large numerical matrix
is in now way particularly slow.
3. Illustration of the symbolic capabilities
Suppose we are interested in
expressing the general form of a matrix representing a rotation of angle
around an axis defined
by a unit vector u. Of course, such simple objects are immediately
available in the set of predefined tools. However, we will show as an example
how to define and use it symbolically. For avoiding lengthy developments beyond
the scope of this note, several technical aspects will not be detailed, or will
even be left in the shadow, when the context is sufficiently clear or when this
does not compromise understanding. Everyone interested in details should search
in the on-line help for additional explanations (and accept to spend some
learning time).
We can first make use of the
intrinsic definition of a rotation.
Rotating a vector V by q
around a unit vector u defining
the axis of rotation may be expressed as :
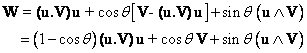(1)
Such an expression has an obvious geometric
meaning in terms of the component of V along the axis of rotation u
(invariant under the rotation), and of
the rotated component of V perpendicular to u. Equation (1) has
an immediate translation in the Mathematica language:
RotVec[u_List,q
_][V_List]:=(1-Cos[q
])*(u.V)*u + Cos[q
]*V + Sin[q
]*Cross[u,V]
(2)
This defines a function Rotvec depending on the
two parameters u and q
and taking V as the
variable. Note that apart for idiosyncratic specificities inherent to any
programming language, the latter definition (2) is easily decipherable. The
nice thing is that (2) can be used symbolically with u defined as
{a
, b
, g
} and V
as {x, y, z} without giving explicit values to the variables. As detailed a
little bit more in the following, the braces { } are the hallmark of any kind
of list in Mathematica and a vector may be considered as a 1D list. One
may thus ask for the result of :
W = RotVec[{a
, b
, g
},q
][{x, y, z}] (3)
which will appear as a list of three linear
forms in x, y and z. By applying the following syntax (which will not be
explained in details here, but see § 6),
m = Map[Coefficient[#,{x,y,z}]&,W] (4)
the coefficients of x, y and z are obtained,
which after an additional line of code for factorization (not shown here),
yields the sought after rotation matrix
m :
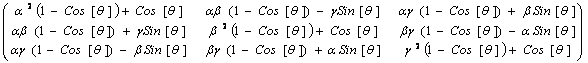(5)
Note that the latter expression was not hand-written,
but is a direct output of Mathematica. In order to achieve giving a
glimpse on the symbolic capabilities, we will simply show the result of the
function Eigenvalues applied to the
latter matrix m:
Eigenvalues[m]
/.(
a
^2+b
^2+g
^2)®
1 (6)
In (6), the syntax /.(a
^2+b
^2+g
^2)®
1 is a ‘replacement rule’ forcing u
to bea unit vector. As output of
(6), one readily obtains the list of eigen values:
{1, Cos[q
]-iSin[q
], Cos[q
]+iSin[q
]} (7)
This is a useful reminder that
and
, as well as 1, are eigen values of a matrix of rotation by
an angle q
. Asking for the corresponding eigen
vectors with:
FullSimplify[Eigenvectors[m]]
/.(
a
^2+b
^2+g
^2)®
1 (8)
one obtains as output:
(9)
containing, first the expected vector {a
/g
, b
/g
, 1}
parallel to u ={a
, b
, g
}, as well
as those corresponding to the complex eigen values
and
. In (9), FullSimplify is a call to a simplification procedure of wide use for algebraic
expressions.
4. Description of the basic set of utilities available in
the package
We will
only give a brief list of essential utilities.
4.1
Reading (and making) files
PDB coordinate and reflection files
Denzo and CCP4 MTZ reflection files (MTZ files
can be read and written)
CNS and CCP4 electron density maps (CCP4 maps
can be read and written)
4.2
Atomic model representation
A simple graphics representation of an atomic
model is available. For now, this is only a very crude option for the sake of
verification of the coordinates in use.
4.3
Crystallographic data bases (from CCP4)
All symmetry operations.
Limits of asymmetric units and alternative
origins for each space group.
All atomic scattering factors.
4.4
Elementary calculations
Orthogonalization and deorthogonalization
matrices.
Metric tensor in reciprocal space, calculation
of resolution.
Sorting out centric and general reflections.
4.5
Phase and map calculation
Phase and map calculations can be made either internally
(i.e. as a Mathematica procedure), or by launching from within Mathematica
in a ‘user-transparent’ way a CCP4 calculation (i.e. without any need of
typing a DOS or Unix line of command or of using the CCP4 GUI).
4.6
Plotting and graphics representation
Mathematica provides a great deal about plotting data and
graphics representation. There exists many possibilities for exporting and
importing graphics. This aspect is not secondary because working in such an
environment makes graphics representation immediately available for anything.
Map section contouring, for example, is extremely efficient and fast. In the
present state, however, it is not possible to make plots with oblique axis as
requested for non orthorhombic space groups. It is intended to remove this
limitation in the next release of the package.
4.7
On-line help
It is an important feature that all tools in
the package are referenced in the on-line help, exactly as for any ‘official’ Mathematica
tool. It should also be emphasized that this on-line help is not only an
exhaustive list of the syntactic rules, but that it also allows a dynamic test
of them. For example, when searching for how a call to CCP4 is made for
calculating an electron density map, the user has the possibility, within the help itself, of running real examples and changing parameters.
5. Organization of data
One major tool in Mathematica
is the ‘list’. As previously mentioned, a ‘list’ is simply notated by braces
enclosing different elements separated with commas (e.g. FirstPrimes = {1,2,3,5,7}; one particular element, for example
5 at the fourth position, is retrieved as FirstPrimes[[4]]). It can be viewed as representing any
collection of any objects structured in any possible way. A list can be as
simple as a 1D vector of numbers (atomic coordinates are obviously structured
as a list {x,y,z}), but can collect symbols, e.g.
, or even symbolic rules. It can be structured to any depth,
regularly as a m´
n
matrix, or without any regularity. It is of such use that many powerful tools
exist to manipulate them. Simple examples will illustrate its usage.
5.1
Definition of ‘parallel lists’
What we
call ‘parallel lists’ is of extremely common usage in the package. Two lists
are said ‘parallel’ if each element in one list corresponds to the element at
the same position in the other list. As a consequence, ‘parallel lists’ must
have the same length. The importance of this notion is made very clear in the
following with the organization of atomic coordinates or of reflections. For
example atomic coordinates and the corresponding atomic names are stored in
‘parallel lists’. Importantly, the substructure of each list may be different;
one only requires that the two lists be identically structured at the first
level.
One very important function allowing
to make a single list from two parallel lists or, alternatively, to split a
single list into parallel lists is TRANSPOSE . For example, with the two
parallel lists:
hkl = {{h1,k1,l1},{h2,k2,l2},{h3,k3,l3},…};
F = {F1, F2, F3,…};
one obtains a single list:
hklF =
{{{h1,k1,l1},F1},{{h2,k2,l2},F2},{{h3,k3,l3},F3},…};
with the syntax:
hklF = Transpose[{hkl,F}];
Conversely, hklF
may be splitted into hkl and F with the
syntax:
hkl = Transpose[hklF][[1]];
F =
Transpose[hklF][[2]];
Note that the semicolon at the end of each
definition tells Mathematica not typing the result on the screen (which
may correspond to huge outputs with long lists).
5.2
Atomic coordinate organization
Atomic
coordinates are naturally organized as a
list with the hierarchy :
{chain(s) {residues {atoms}}}.
If a list of coordinate is obtained from a PDB
file, by default it is named XYZ, and XYZ[[2]] will refer to the second chain, XYZ[[2,3]] to its third residue, and XYZ[[2,3,1]] to the first atom of the third
residue of the second chain. XYZ[[2,3,1]] thus corresponds to a list of
atomic coordinates of type {X,Y,Z}. All other
relevant pieces of information for each atom are stored in different ‘parallel
lists’. For example the list named QB stores occupancies Q and temperature factors B, and QB[[2,3,1]] refers to the two-value list {Q,B} for the atom with coordinates XYZ[[2,3,1]]. The same holds true for the lists ATOMNAMES and ATOMTYPES. For the sake of consistency and
programming generality the same structure is always used, even if one level is
not useful in a particular case. For example, for a molecule with two different
chains the coordinates are naturally stored as {{chain1},{chain2}}, but for a
molecule with one single chain they are still kept as {{chain1}}, not {chain1}.
5.3
Symmetry operation organization
All space
groups are stored in a list of sublists, with one sublist for each space group.
The necessary information was obtained from the CCP4 package. The information
for a specific space group is retrieved as:
InfoSpaceGroup["P21"] (or InfoSpaceGroup[4]) (10)
which yields as output the following list:
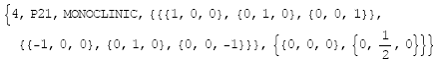(11)
In the fourth position are stored the symmetry
matrices and in the fifth position the corresponding translations.
5.4
Reflection organization
Reflections are stored in ‘parallel
lists’. One of these lists, commonly named hkl, stores Miller indeces as a list of individual {h,k,l}. Intensities, amplitudes, sigmas, phases, etc… are stored at will of
the user in ‘parallel lists’. Note that the user is free of grouping whatever
he wants in a single list. For example, if F’s and sigmas are grouped to form FSigma, FSigmais madeof elements {F(h,k,l),SigmaF(h,k,l)}. The two lists hklandFSigmaare obviously parallel.
5.5
Electron density maps
Electron density maps in 3D are
stored in lists of sections, each section being a list of rows, and each row a
list of values. They can be readily obtained as such by a call to CCP4 from
within Mathematica:
DensityMap =
CalcMapCCP4[hkl,F,PHI,UnitCell,SpaceGroup,(Options)](12)
where hkl is a list of Miller indeces, and F and PHI the parallel lists of structure factor amplitudes and phases. UnitCellis a list of the form {a, b, c, a
, b
, g
} andSpaceGroupa character string of the form “P21”. All options for CCP4 map
calculation can be given in a list of Options.
6. Examples of ‘elementary’
manipulations
A few examples will be worked out in
some details to illustrate the usage of the stored data, as well as some basic
features of the philosophy of Mathematica programming, and the density
of the code. As already stated before, several technical aspects will not be
developed, or will be left in the shadow, when the context is sufficiently
clear or when this does not compromise understanding.
6.1
Manipulating electron density maps
Manipulating an electron density map
as a whole is a trivial operation in Mathematica. For example, applying
a mask mask onto a density map map for
solvent flattening is obtained as:
FlatMap = mask*map ; (13)
Predefined interpolation tools allow to
determine functional approximations of a map very efficiently. This allows, for
example, to resample a map at will on any ‘skewed’ mesh for molecular
replacement. Such tools seem promising, also in the scope of molecular
replacement, for applying smooth distortions on a map by using normal-mode-like
methods as already described (Delarue & Dumas, 2004; Suhre &
Sanejouand, 2004). We think that there exist considerable possibilities in this
area because of the great efficiency of many preexisting tools in Mathematica.
This will not be detailed further here.
6.2
Calculating scattering factors
The scattering factor of a
particular atom type is obtained as InfoFormFactor[“atomtype”], “atomtype” representing a character string. For example, InfoFormFactor[“Ca”] returns the information for calcium:
{Ca,{{8.6266,10.4421},{7.3873,0.6599},{1.5899,85.7484},{1.0211,178.437},{1.3751,0.}},{0.341,1.286,0.203,0.306}}
where the parameters for the usual four-gaussian
approximation (International Tables, Vol 4, 1974) are returned as the second
element of the latter list, that is to say:
GaussCa
= InfoFormFactor[“Ca”][[2]];
(14)
which contains the following numerica values:
{{8.6266,10.4421},{7.3873,0.6599},{1.5899,85.7484},{1.0211,178.437},{1.3751,0.}}
Summing up the five functions
(with
), corresponding to the five elements of form {Qi, Bi} in the latter list GaussCa (note that the fifth Gaussian function is in fact a constant), can be performed with the
self-explanatory usual ‘procedural’ syntax:
Sum[g[GaussCa[[i,1]], GaussCa[[i,2]], s], {i, 1, 5}]
(15)
Although it appears quite cryptic at
first sight, it is much more preferable to use the following functional method.
First, one ‘maps’ the function g onto the list GaussCa, that is onto each element of GaussCa:
Map[g[#[[1]],#[[2]],s]&, GaussCa] (16)
which yields as result the following list:
{Q1*Exp[-B1 s^2], Q2*Exp[-B2 s^2], Q3*Exp[-B3 s^2], …}
(17)
with Q1=8.6266, B1=10.4421, Q2=7.3873, B2=0.6599,etc…In (16) the
syntax #[[1]] and #[[2]] stand for the arguments of a
function (here, the function g) by referring to each element of
the list it is mapped onto. In the present case, each element of GaussCa is a sublist of the kind {Qii,
Bi}, and #[[1]] thus refers to Qi, and #[[2]] to Bi. Note also the character ‘&’ that is the mark of the end of the
definition of what is called a ‘pure function’ in Mathematica. The usage
of # for referring to variables, and of ‘&’ for marking a pure function
cannot be dissociated. This syntax allows using a function without predefining
it. In some sense, a pure function may be viewed as a ‘disposable’ function.
For example, the sum of the five functions
can readily be invoked
as follows (note the use of the trace operator Tr for summing up the elements of a 1D
list):
diffus[GaussX_List][s_]:=Tr[Map[#[[1]]*Exp[-#[[2]]*s^2]&,GaussX] (18)
to define the value of the scattering factor of
any element X with parameters stored in GaussX. The form used in (18), i.e.
the mapping of a pure function onto a list, is equivalent to that used in (15)
as far as the result is concerned, but (18) has the advantage of yielding very
often the most concise code, and of never requesting explicit handling of the
limits of a list. Since Mathematica has symbolic capabilities, GaussX may be replaced with a list of symbols like {{Q1,B1},{Q2,B2},{Q3,B3},{Q4,B4},{c,0}} to obtain a purely analytic
expression.
6.3
Sorting out centric and general reflections
As
another example, we will consider a concise way (and even also a very concise
way) of extracting all centric reflections from a list of reflections. A
reflection {h,k,l} is centric if there exists a symmetry
operation whose matrix m is such that :
{h,k,l} +
Transpose[m].{h,k,l} = {0,0,0}
(19)
One thus first maps the pure function (# + Transpose[m].# )&onto
the full list of reflections hkl and then searches for positions of {0,0,0} in the result; this can be made a
function of m and hkl as follows:
CenPos[m_List,hkl_List]:=Position[Map[#+Transpose[m].#&,hkl],{0,0,0}](20)
Then, one can map this new function onto the
list Sym of all symmetry matrices for the space group
of interest (see § 5.3), and consider the union of the whole set of
positions:
CenPositions = Apply[
From this list of positions in hkl, one can then extract all centric reflections from hkl:
Centric = Map[Extract[hkl,#]&, CenPositions];
In the package, these three lines of code are
grouped into a callable function (named CentricHKL), and the list of centric reflections is returned at once as:
Centric = CentricHKL[hkl,SpaceGroup];
In fact, these three lines of code can even be
reduced to a bit cryptic ‘one-liner’:
Union@@Table[Cases[hkl,_?(#+Transpose[Sym[[i]]].#=={0,0,0}&)],{i,2,Length[Sym]}]
(21)
This is only shown here to illustrate how
concise the code can be and this will not be discussed further. The former
three-line version is used in the package because it turns out to be faster.
This example is only a very short glimpse at the powerful capabilities of Mathematica
for sorting and extracting information from any kind of lists.
7. Conclusion
In its present state, BioCrystallographica
allows performing original methodological tests because all basic tools for
doing crystallography are available and embedded in a very powerful
environment. We hope a significant number of persons among those interested in
methods will participate in developing it. We consider as an interesting goal
the extension of links between BioCrystallographica and other crystallographic softwares as this is already done with CCP4.
Clearly, reinventing the wheel and reprogramming already available tools has no
interest, but making them available in an original powerful environment is of
great interest. For the time being the link to external programs (like CCP4)
has been tested under Windows. Extending this functionality to Unix-, or
Linux-based platforms should be straightforward.
The package is freely available for
academic users upon request. We have made a web
site to
illustrate our work with Mathematica in crystallography. For the time being,
it shows essentially teaching applications. We plan to enhance the
functionalities in a near future.
References
COLLABORATIVE
COMPUTATIONAL PROJECT, NUMBER 4. ‘The CCP4 Suite: Programs for Protein
Crystallography’. (1994) Acta Cryst. D50, 760-763.
Brünger, A.T.,
Delarue, M. & Dumas, P. ‘On the use of
low-frequency normal modes to enforce collective movements in refining
macromolecular structural models’. (2004) PNAS 101, 6957-6962.
International Tables for X-ray crystallography,
Vol 4 (1974) The Kynoch press,
Suhre, K & Sanejouand Y.H. ‘On the
potential of normal mode analysis for solving difficult molecular replacement
problems’, (2004) Acta Cryst. D60, 796-799.