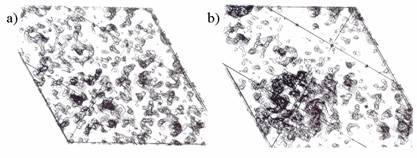
Fig.1.
Comparison of ten sections of the 4.5Å map of yeast tRNA
before (a) and after (b) the inclusion of 28 low-resolution terms whose phases
were determined by matrical methods (Podjarny, Schevitz & Sigler
(1981), Acta Cryst. A37, 662-668).
Retrieval of lost reflections in high resolution Fourier syntheses by a
‘soft’ solvent flattening.
by Natalia L. Lunina1,
Vladimir Y. Lunin1 & Alberto D. Podjarny2
1Institute of Mathematical Problems
of Biology, Russian Academy of Sciences, Pushchino,
Moscow region, 142290 Russia; lunina@impb.psn.ru
.
2UPR de Biologie
Structurale, IGBMC, BP 163, 67404 Illkirch,
CU Strasbourg, France, podjarny@igbmc.u-strasbg.fr.
1. Abstract.
Accurate studies of a high
resolution Fourier synthesis require the full set of structure factors to be
used when calculating the synthesis. Structure factors with unknown phase or
even with unknown amplitude may be restored with a reasonable accuracy through
density modification methods. For the case of Aldose Reductase, measured at 0.9
A resolution, a special type of the solvent flattening
was tested for restoring about 20 000 (10% of the full set) structure factors
in 0.9Å resolution zone. This flattening is based on the connectivity
analysis of the Fourier synthesis map and is applied to small ‘drops’ only.
2.
Model-free structure factors retrieval.
The quality of Fourier syntheses maps depend
both on the accuracy of magnitude and phase values of structure factors and on
the completeness of the set of structure factors used to calculate the map. The
impact of a relatively small number of lost reflections on the quality of low
resolution syntheses was demonstrated in a number of papers and different ways
to restore these lost values were discussed (Podjarny,
Schevitz & Sigler, 1981; Lunin,
1988; Lunin & Skovoroda,
1991; Urzhumtsev, 1991). Figs. 1-3 give some examples
of such restoring.

Fig.1.
Comparison of ten sections of the 4.5Å map of yeast tRNA
before (a) and after (b) the inclusion of 28 low-resolution terms whose phases
were determined by matrical methods (Podjarny, Schevitz & Sigler
(1981), Acta Cryst. A37, 662-668).

Fig. 2. (a)
Initial (SIR) 8Å map for the elongation factor G and (b) the map with
additional 29 low resolution reflections restored by the Double Step Filtration
method (Urzhumtsev (1991), Acta
Cryst. A47,
794-801.
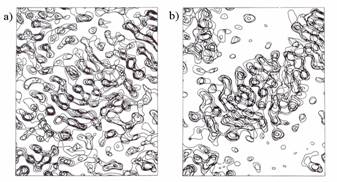
Fig. 3. (a) Initial 4 Å map
for g-crystallin IIIb and (b) the map
with additional structure factors restored from electron-density histogram (Lunin & Skovoroda (1991), Acta Cryst., A47, 45-52.
The
importance of complete data sets is not restricted to low resolution only, but
is also true at subatomic resolution, where the electron density distribution
in itself becomes the subject for studies. The missing reflections can be
important when investigating these fine features at low contour levels. At the
same time, the positions of peaks in high resolution Fourier syntheses are less
sensible to missing reflections and may be found correctly even when some
structure factors are absent (see Fig.5, 6 for comparison).
The retrieval of the lost structure
factors may consist in either determination of their phases (if the reflection
magnitude was measured, but was not phased) or restoring both the magnitude and
the phase of structure factor (if the reflection was not measured). We discuss
below the possibility of restoring both magnitudes and phases of the lost
structure factors in the ‘nominal’ resolution
zone. The extrapolation of data to higher resolution zones (Karle
& Hauptman, 1964; Langs, 1998; Xu & Hauptman, 2000) is out of the scope of these
notes. In high resolution density studies an atomic model of the studied object
usually exists and might be used to calculated values of the lost structure
factors. Nevertheless, such structure factors are highly biased towards the
model used and do not usually show new features of the real electron density in
a crystal, which can differ from the atomic model density. These circumstances
require the developing of ‘model-free’ methods of calculation of structure
factors not-determined in an experiment. Density modification methods (for a
review, see e.g. Podjarny,
Rees & Urzhumtsev, 1996, e.g.) provide ways to do this.
3. ‘Soft’ solvent flattening
The
outlines of the procedure used are general for iterative density modification
methods. Each cycle of the procedure consists of the following steps:
The last step is different from the usual one
for unmeasured reflections, for which the whole calculated structure factor is
used to update the current values.
In our tests we applied the density
modification based on new type of density flattening in the solvent region. The
solvent density flattening belongs to the oldest methods of density
modification (Bricogne, 1974; Wang, 1985) and is one
of the most frequently used tools for phase improvement. Nevertheless, the
usual goal of its application is phase refinement and only rarely magnitude
restoring. The other feature of the usual approach is that the all density in
the assigned solvent region is flattened. At the same time there may exist real
density features in this region, which are not interpreted yet. Such density
might be removed from the maps as a result of the ‘total’ solvent flattening.
The procedure discussed below uses a softer type of density modification in the
solvent region. It is based on the observation that the small drops in the maps
represent usually noise, while real structural features are represented by more
extended regions. The modification discussed consists in reducing of density
corresponding to sharp narrow peaks, while the larger ‘blobs’ of a density in
the solvent region are left unchanged. Such procedure combines the features of
traditional density modification methods with the connectivity based phasing (Lunin, Lunina & Urzhumtsev, 1999, 2000).
Every
step of density modification is defined by:
First, the set of the points in the unit cell
with the synthesis values ![]() is analyzed. The goal
of the analysis is to find the number and sizes of connected isolated
components in this set. If a component has no common points with the molecular
region it is considered as a solvent ‘drop’. If the size of this drop is small
enough (smaller than
is analyzed. The goal
of the analysis is to find the number and sizes of connected isolated
components in this set. If a component has no common points with the molecular
region it is considered as a solvent ‘drop’. If the size of this drop is small
enough (smaller than ![]() ) the density values for all points in this drop are replaced
by
) the density values for all points in this drop are replaced
by ![]() . All other points in the unit cell keep their previous
values.
. All other points in the unit cell keep their previous
values.
The
parameters of the modification are generally updated from step to step.
4. Test object.
The
tests were performed with a high resolution data set for aldose reductase. The
crystals of human aldose reductase belong to space group P21 and
have unit cell parameters a=49.97,
b=67.14, c=48.02 Å, b=92.2o. There is one molecule per asymmetric unit cell with
the molecular weigh about 36 kDa. The crystals
diffract to 0.66 Å (Lamour et al., 1999; Howard et al.,
2000, Sanishvili et al, paper in preparation) and the
structure was refined using SHELX (Howard et al, paper submitted) allowing to
collect MAD data to 0.9 Å resolution. This data was phased using SHARP (D'Allantonia et al, paper in preparation). Such high
resolution allows starting density distribution studies (Guillot
et al., 2000), which were carried
before mostly with small molecules. Our tests were done at 0.9Å
resolution, starting from MAD-phased data set.
All the theoretically possible
reflections in 0.9Å resolution zone were divided in three sets. Set I
consisted of reflections with the measured magnitude and the phase determined
by MAD-method. Set II consisted of reflections whose magnitudes were measured,
but the phases were not determined. Set III consisted of reflections with
unmeasured magnitudes. The last was composed mostly from the very low
resolution reflections and reflections of the highest resolution shell (see
Table 1).
To
calculate a Fourier synthesis, which represents correctly the electron density,
it was necessary:
In the first half of our test for reflections
in Set II the goal was changed for restoring both magnitudes and phases. Then,
the restored magnitudes for Set II were replaced by the observed ones, and the
phases only were refined further. The reason for this was that at the first
cycles of structure factors improvement the quality of the newly defined phases
is very poor (see Fig.4.) and the use of real magnitudes values deteriorated
the process. The restored magnitudes were significantly less than corresponding
experimental values and this might be considered as a kind of weighting of such
reflections.
Table 1. Distribution of reflections in
resolution shells.
|
Resolution
shell |
Set
I: MAD-phased |
Set
II: measured, unphased |
Set
III: unmeasured |
|
49.28-4.01 |
2476 |
148 |
31 |
|
4.01-2.84 |
4454 |
248 |
0 |
|
2.84-2.32 |
5723 |
344 |
0 |
|
2.32-2.01 |
6803 |
356 |
0 |
|
2.01-1.80 |
7707 |
408 |
1 |
|
1.80-1.64 |
8413 |
485 |
0 |
|
1.64-1.52 |
9019 |
706 |
0 |
|
1.52-1.42 |
9835 |
589 |
0 |
|
1.42-1.34 |
10455 |
606 |
1 |
|
1.34-1.27 |
11058 |
706 |
0 |
|
1.27-1.21 |
11596 |
708 |
0 |
|
1.21-1.16 |
12162 |
734 |
0 |
|
1.16-1.12 |
12624 |
786 |
0 |
|
1.12-1.08 |
13085 |
817 |
0 |
|
1.08-1.04 |
13579 |
885 |
0 |
|
1.04-1.01 |
14031 |
888 |
0 |
|
1.01-0.98 |
14446 |
978 |
0 |
|
0.98-0.95 |
14719 |
1072 |
94 |
|
0.95-0.92 |
14582 |
1272 |
474 |
|
0.92-0.90 |
10292 |
1348 |
5082 |
|
Total |
207
059 |
14 084 |
5
683 |
5. The choice of parameters of the modification.
The
same mask of the molecular region was used during the whole test. It was
constructed as the joint region formed by spheres with the radius 0.8Å centred
at the atomic centres. The influence of the sphere radius on the progress in
structure factors restoring will be discussed elsewhere.
For
every cut-off level it is possible to estimate the mean number of points in the
‘blobs’ corresponding to the recognized water molecules. Approximately half of
this value was used to set the parameter![]() , which defines the minimal allowed size for the drops in the
solvent region.
, which defines the minimal allowed size for the drops in the
solvent region.
In
the total, 1000 steps of iterative structure factors improvement were
performed. The procedure was divided into several series of 50-100 steps in
average. In every series, the cut-off level ![]() decreased step by step
varying in the range from 1.5 – 1.2 ‘sigmas’ in first
series to 2.2 – 0.45 in last ones.
decreased step by step
varying in the range from 1.5 – 1.2 ‘sigmas’ in first
series to 2.2 – 0.45 in last ones.
6. Test results
The structure factors calculated
from the atomic model cannot be considered as the final goal of the restoring
because one of the purposes of high resolution density studies is to find the
difference between the real density distribution and that calculated from the
model. Nevertheless, these values may serve as a good reference values when
restoring structure factors. The increase of the correlation of restored
structure factors (of the Set II) with the model structure factors is shown at
Fig. 4 for different resolution shells. This figure shows that the quality of
restored structure factors significantly grows in the course of modification.
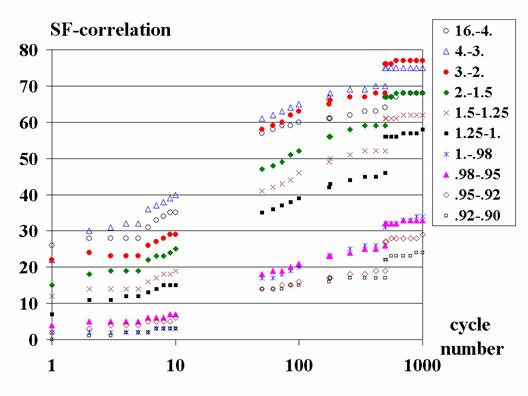
Fig. 4. The growth of accuracy of
the restored structure factors for the Set II in the course of the restoring is
shown for different shells in the reciprocal space. The shown SF-correlation
was calculated as
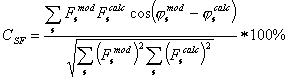
where ![]() are the structure
factors calculated from the atomic model and
are the structure
factors calculated from the atomic model and ![]() are calculated from
the modified density maps.
are calculated from
the modified density maps.
Sections of Fourier syntheses maps before and
after modification are shown in Figs. 5 and 6. In contrast to high cut-off
values (Fig.5), the low cut-off maps are sensible to the completeness of the
set of structure factors and to the phases accuracy
(Fig.6).
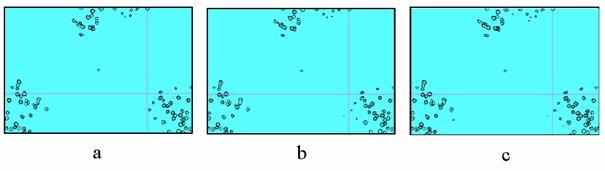
Fig. 5. Aldose reductase Fourier syntheses of 0.9 Å resolution,
‘3-sigma’-cutoff. a) MAD-phased synthesis, 10% of reflections are
absent; b) refined phases, 10% of reflections are still absent; c) refined
phases, the restored values of structure factors are added for 10% of
reflections absent in (a) and (b). The difference between the syntheses is
extremely small (see Fig.6 for comparison).
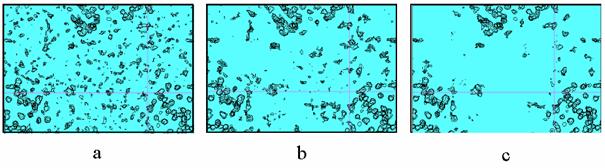
Fig. 6. Aldose reductase Fourier syntheses of 0.9 Å resolution,
‘1-sigma’-cutoff. a) MAD-phased synthesis, 10% of reflections are
absent; b) refined phases, 10% of reflections are still absent; c) refined
phases, the restored values of structure factors are added for 10% of
reflections absent in (a) and (b).
Fig. 7 shows the decreasing of the
number of drops in the solvent region from the MAD-phased synthesis to the
final one.
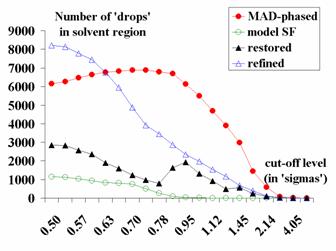
Fig. 7. The number of isolated
components in the solvent region for different Fourier syntheses of 0.9 Å
resolution: the start MAD-phased synthesis; the synthesis calculated with
structure factors obtained from the atomic model (model SF); the synthesis with
refined phases, but 10% of reflections absent (refined); the synthesis with all
reflection restored and refined (restored).
One
of the possible measures of progress in the structure factors restoring is the
growth of mean value of restored structure factor magnitudes in comparison with
the mean value of the measured magnitudes in the corresponding resolution shell
(Fig. 8).
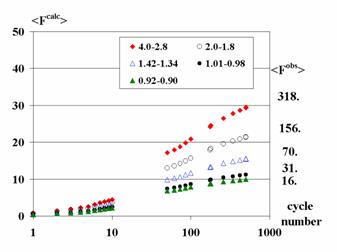
Fig. 8. The growth of mean values
of calculated from the modified syntheses magnitudes in the course of the
restoring for the Set II (several resolution shells only are shown. The mean
values of the observed magnitudes in the considered shells are shown at the
right.
The
correlation of restored magnitudes with the measured ones (if they are known)
may serve as control value too (will be discussed elsewhere).
7. Conclusions
The test results show that a density
modification allows restoring a large number of unmeasured or unphased structure factors. These structure factors improve
the image of density distribution map and may be very important in high
resolution density studies. Obviously, more advanced density modification
techniques may be used as well to improve the power of the method.
8. Acknowledgments
This
work was supported by CNRS-RAS collaborative program and RFBR grant 00-04-048175. The authors thank Alexandre Urzhumtsev and Claude Lecomte
for valuable discussions and possibility to use LCM3B resources. We thank also Andrzej Joachimiak, Ruslan Sanishvili, for their help
in collecting the Aldose Reductase data, and Thomas Schneider, Fabio D’Allantonia and George Sheldrick
for their collaboration in refinement and MAD phasing.
Bricogne,
G. (1974). Geometric Sources of Redundancy in Intensity Data and Their Use for
Phase Determination Acta Cryst, A30, 395-405.
Guillot, B., Jelsch,
C., Muzet, N., Lecomte, C.,
Howard, E., Chevrier, B., Mitschler,
A., Podjarny, A., Cousson,
A., Sanishvili, R. & Joachimiak,
A. (2000). Multipolar
refinement of aldose reductase at subatomic resolution. Acta Cryst.
A56 (Supplement),
s199.
Howard,
Karle, J. & Hauptman, H. (1964). Positivity, Point Atoms, and Pattersons. Acta Cryst. 17, 392-396.
Lamour, V., Barth,
P., Rogniaux, H., Poterszman,
A., Howard, E., Mitschler, A., Van Dorsselaer, A., Podjarny, A.
& Moras, D. (1999).Production of crystals of
human aldose reductase with very high resolution diffraction. Acta Cryst. D55, 721-723.
Langs, D.A. (1998). Reinvestigation
of the Use of Patterson Maps to Extrapolate Data to Higher Resolution. Acta Cryst.
A54, 44-48.
Lunin, V. Yu. (1988). Use of
the information on electron density distribution in macromolecules. Acta Cryst.
A44, 144-150.
Lunin, V. Yu. & Skovoroda, T. P. (1991). Frequency-restrained
structure-factor refinement. I. Histogram simulation. Acta Cryst.
A47,45-52.
Lunin, V. Y., Lunina,
N. L. & Urzhumtsev, A. G. (1999). Seminvariant density decomposition
and connectivity analysis and their application to very low resolution
macromolecular phasing. Acta Cryst.
A55, 916-925.
Lunin, V. Y., Lunina,
N. L. & Urzhumtsev, A. G. (2000). Connectivity
properties of high-density regions and ab initio phasing at low resolution. Acta Cryst.
A56, 375-382.
Podjarny, A.D., Schevitz,
R.W. & Sigler, P.B. (1981). Phasing Low-Resolution
Macromolecular Structure Factors by Matrical Direct
Methods., Acta Cryst. A37, 662-668.
Podjarny, A.D., Rees, B. & Urzhumtsev, A.G. (1996). Density Modification in
X-Ray Crystallography. In “Methods
in Molecular Biology”, 56,
205-226.
Urzhumtsev, A. G. (1991). Low-resolution
phases: influence on SIR syntheses and retrieval with double-step filtration. Acta Cryst.
A47, 794-801.
Wang,
B.C. Resolution of phase ambiguity (1985). Methods
Enzymol., 115, 90-112.
Xu, H. & Hauptman, H. A. (2000). On the extrapolation of the
magnitudes |E| of the normalized structure factors E. Acta Cryst.
A56, 284-287.