Variation of solvent density and low-resolution ab initio phasing

 

Andrei Fokine

 

LCM3B, UMR 7036 CNRS, Faculté des Sciences, Université Henry Poincaré, Nancy I, 54506 Vandoeuvre-lés-Nancy, France

e-mail: fokine@lcm3b.uhp-nancy.fr

 

 

Abstract

The bulk solvent plays a key role in the direct phasing at low resolution. The connectivity-based phasing method has been tested for the crystal of the tRNA^Asp-aspartyl-tRNA synthetase complex. The neutron diffraction data have been measured for different solvent contrast masking different components of the crystal. The obtained low resolution images are perfectly correlated with the solvent level.

 

 

1. Introduction

 

Low-resolution Fourier syntheses provide a very useful information about molecular packing and the shape of molecules. Such low-resolution images can be obtained by direct phasing of a single set of experimental modules (Lunin et al., 2000a). The information supplied by ab initio phasing methods is inestimable when conventional phasing techniques do not work. The low resolution phases can be used as a starting point for phase extension. Additionally, the knowledge of molecular position can facilitate the solution of molecular replacement problem. Here the ab initio phasing method based on topological properties of density maps is considered. This method employs the expected connectivity of a Fourier synthesis as an additional information to obtain phases (Lunin et al., 2000b). Among the known low-resolution direct phasing techniques this method is considered to be the most promising. There are several examples when this method allowed to determine molecular positions, molecular shapes (Lunin et al., 2000a; Lunin et al., 2000b) and even secondary structure elements (Lunin et al., 2002).

Macromolecular crystals contain a large part of the bulk solvent whose contribution to low-resolution reflections is very important. At low resolution the assumption of a uniform scattering density distribution in the solvent region is held well and the value of solvent scattering density can be estimated from the composition of crystallization solution. In X-ray structural analysis the electron density of the bulk solvent varies in the small range 0.33 – 0.41 e/ų (Kostreva, 1997). The solvent electron density is close to the average electron density of a typical protein 0.43 e/ų (Kostreva, 1997; Carter et al., 1990) and less than that of DNA / RNA. In neutron diffraction experiment, the solvent scattering density can be varied in a large range by changing the ratio of D₂O / H₂O in the mother liquor. The solvent scattering density can be made lower equal or greater than the average scattering density of a protein or DNA / RNA. Such possibility of choice of an appropriate solvent scattering density is the basis of the method of contrast variation (Jacrot, 1976). 

The connectivity properties of low-resolution Fourier syntheses essentially depend on the solvent contribution. Therefore, the results of direct phasing which uses these properties as the selection criterion depend on the solvent scattering density. The purpose of the current work was to study the role of the bulk solvent in the connectivity-based direct phasing.

In this paper we present the results of ab initio phasing of three sets of neutron diffraction data from the same crystal of the tRNA^Asp-aspartyl-tRNA synthetase complex (Moras et al., 1983) measured for different solvent contrast masking different components of the crystal. The obtained low resolution images are perfectly correlated with the solvent scattering density level.

 

 

2. Phasing method

 

The basic idea of the connectivity based phasing method (Lunin et al., 2000b) consists in the observation that topological properties of high density regions of the Fourier syntheses are different for properly phased syntheses and for those calculated with random phases.

Let ρ(r) be a Fourier syntheses calculated on a finite grid and N be a number of grid points in the unit cell. The high density region Ω(α), corresponding to the relative volume α is defined as a set of αN grid points of highest density. For a correctly phased low-resolution synthesis this region would be composed of a small number of isolated ‘blobs’ corresponding to independent molecules if the cut-off level α is chosen appropriately. The number of these blobs is usually equal to the number of molecules in the unit cell. The blob volumes (measured in the number of grid points) must be equal between themselves if all molecules are linked by crystallographic symmetries and must be approximately equal if non-crystallographic symmetry is present. On the other hand, randomly phased syntheses are likely to show infinite merged regions or a large number of ‘drops’.

The phasing procedure consists in following steps.

1)      A large number of random phase sets are generated. The phases are generated with the uniform distribution at the beginning of the procedure or in accordance with a known phase distribution if this information is already available.

2)      For every generated phase set the Fourier synthesis is calculated using the experimental structure factor modules.

3)      The high density regions of each calculated synthesis are subjected to connectivity analysis in order to determine the number of separated connected components in the unit cell and to calculate their volumes.

4)      If high density regions consist of a desired number of components, the corresponding phase set is considered as admissible and is stored, otherwise the phase set is rejected.

5)      After a reasonable number (about one hundred) of admissible phase sets have been selected, they are averaged in order to produce the corresponding ‘best’ phases  and figures of merit , which reflect the spread of the admissible phase sets

 .                                           (1)

Here M is the number of selected phase sets and  is the value of phase of the structure factor with the index h in the j-th selected phase set. It should be noted that the optimal alignments of the phase sets in accordance with the permitted origin shifts (Lunin & Lunina, 1996) must be performed before averaging.

 

 

The phasing method is described in more details in Lunin et al. (2000b).

 

 

3. Test object

 

Cubic form of tRNA^Asp-aspartyl-tRNA synthetase complex

 

The crystals of the cubic form of the tRNA^Asp-aspartyl-tRNA synthetase complex belong to the space group I432 (48 asymmetric unit / unit cell) with a unit cell parameter of 354 Å. The asymmetric unit contains one protein homodimer and two molecules of tRNA. The crystals contain 82% of the bulk solvent. The protein and tRNA molecules occupy 14 and 4 % of the unit cell respectively. The structure was solved by molecular replacement (Urzhumtsev et al., 1994) using 15-8 Å resolution X-ray diffraction data and high resolution (3 Å) model of the complex obtained from the orthorhombic crystal (Ruff et al., 1991).

 

Neutron diffraction data

 

Three sets of neutron diffraction data, all complete at low resolution (from infinity to 24 Å), were measured for the same crystal of the complex with different concentrations of D₂O in the mother liquor (Moras et al., 1983).

The first data set was measured without D₂O in the mother liquor which corresponds to a very low solvent scattering density. This data set corresponds to the full complex molecule.

For the second data set the concentration of D₂O was chosen so that the solvent scattering density was equal to the average density of the protein. Thus the protein was masked by the solvent and only tRNA molecules gave a signal in diffraction.

 The third data set was measured with the solvent scattering density matching the average density of tRNA, therefore this data set corresponds to the protein molecules only.

These three data sets were used for the direct phasing.

 

 

4. Ab initio phasing of experimental neutron data sets

 

It should be noted that for the direct phasing described below we used only a general information (known a priory) such as the number of molecules in the unit cell and the relative unit cell volumes occupied by molecules.

 

Phasing of the data set corresponding to the full complex molecules

 

The crystals contain one densely packed dimer of tRNA^Asp-aspartyl-tRNA synthetase complex in the asymmetric unit. Since the space group I432 has 48 symmetry operations, it is natural to expect that a low-resolution synthesis with correct phases would show 48 blobs of equal volumes corresponding to the complex molecules.

Reflections in the resolution range ∞-45 Å were used  (37 reflections) for phasing and phases were generated with the uniform distribution. The selection criterion was formulated as follows: the high density region occupying 5% of the unit cell (α = 0.05) must be composed of 48 connected blobs of equal volumes. 100 selected variants were stored after about 89000 generations. The selected variants were averaged to produce the ‘best’ phases  and the figures of merit . The ab initio phased synthesis calculated at 45 Å is shown in Fig. 1. From this synthesis, the position of the complex molecules in the unit cell can be determined.  

 

Phasing of the data set corresponding to tRNA molecules

 

The asymmetric unit contains 2 tRNA molecules related by non-crystallographic symmetry and separated at the surface of the complex. It is natural to expect that the low-resolution synthesis with correct phases would show 48 blobs of equal volumes corresponding to the first tRNA molecule and 48 blobs of equal volumes corresponding to the second tRNA molecule. The volumes of blobs corresponding to tRNA molecules related by non-crystallographic symmetry must be approximately equal.

As previously, reflections in the resolution range ∞-45 Å were used for phasing. Phases were generated with the uniform distribution. The selection criterion was formulated as follows: the high density region occupying 3% of the unit cell (α = 0.03) must be composed of 48 connected regions of equal volumes corresponding to the first tRNA molecule and 48 connected regions of equal volumes corresponding to the second tRNA molecule; the ratio of volumes of the connected regions corresponding to different tRNA molecules must be higher than 0.7. It was a priory known that the tRNA molecules occupy 4% of the unit cell therefore the slightly higher cut-off level of 3% was used. About 270000 random phase sets were generated, 100 sets from them satisfied the selection criterion. The corresponding ab initio phased synthesis is shown in Fig. 2. From this synthesis the positions of the tRNA molecules in the unit cell can be determined unambiguously.

 

Phasing of the data set corresponding to the protein molecules

 

Similarly to two previous cases, reflections in the resolution range ∞-45 Å were used and phases were generated with the uniform distribution. The selection criterion was formulated as follows: the high density region occupying 5% of the unit cell (α = 0.05) must be composed of 48 isolated blobs of equal volumes. 100 selected variants were stored after about 50000 generations. The ab initio phased synthesis (Fig. 3) shows clearly the position of the protein homodimer.

 

 

5. Conclusion

 

The current study shows the robustness of the connectivity-based phasing method which was capable to determine unambiguously the position of both tRNA molecules and that of protein homodimer in the tRNA^Asp-aspartyl-tRNA synthetase complex.

The results confirm that the bulk solvent plays the key role in the connectivity-based direct phasing. The phasing of three data set measured from the same crystal led to completely different images depending on the solvent scattering density.

 

The author thanks A. Urzhumtsev, V. Lunin, N. Lunina, E. Chabriere and P. Afonine for useful discussions.

The work was done in the frame of the pole “Intellegence Logiciels” CPER-Lorraine and in collaboration with CCH, Nancy, and was supported by the grant of “Region Lorraine”. The author is a member of GdR 2417 CNRS.

 

 

References

 

Carter C.W., Jr., Crumbley, K.V., Coleman, D.E., Hage, F. & Bricogne, G. (1990). Acta Cryst. A46, 57-68.

Jacrot, B. (1976). Rep. Prog. Phys. 39, 911

Kostrewa, D. (1997). CCP4  Newslett. 34, 9-22.

Lunin, V.Y. & Lunina, N.L. (1996). Acta Cryst., A52, 365-368.

Lunin, V.Y., Lunina, N.L., Petrova, T.E., Skovoroda, T.P., Urzhumtsev, A.G. & Podjarny A.D. (2000^a). Acta Cryst. D56, 1223-1232.

Lunin, V.Y., Lunina, N.L., Urzhumtsev, A.G. (2000^b). Acta Cryst., A56, 375-382.

Lunin, V., Lunina, N., Podjarny, A., Bockmayr, Urzhumtsev, A. (2002) Z. Kristall., in press.

Moras, D., Lorber. B., Romby, P., Ebel. J.P., Giege, R., Lewit-Bentley, A., Roth, M.J.  (1983) Biomol. Struct. Dyn., 1, 209-223

Ruff, M., Krishnaswamy, S., Boeglin, M., Poterszman, A., Mitschler, A., Podjarny, A., Rees, B., Thierry J.-C. & Moras D. (1991) Science, 252, 1682-1689.

Urzhumtsev, A.G., Podjarny, A.D. & Navaza, J. (1994). CCP4  Newslett. 30, 29-36.

 

 

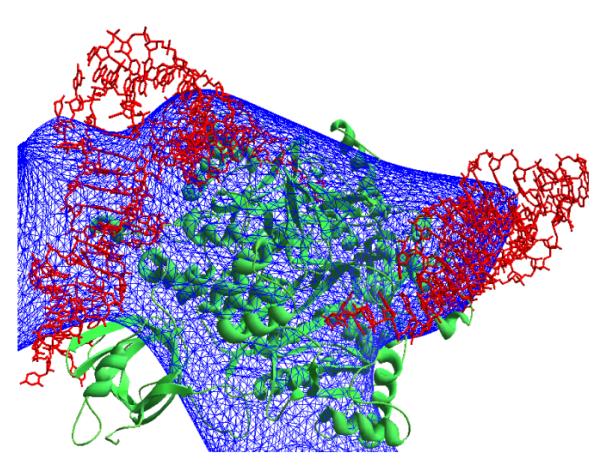
Fig. 1 Synthesis calculated at 45 Å resolution (37 reflections) using experimental modules corresponding to the full complex molecule and phases obtained ab initio.

Protein molecule is shown in green and tRNA molecules are shown in red.

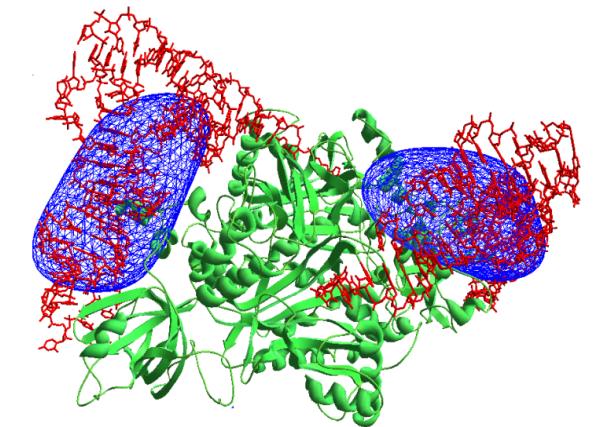
Fig. 2 Synthesis calculated at 45 Å resolution (37 reflections) using experimental modules corresponding to the tRNA molecules and phases obtained ab initio.

Protein molecule is shown in green and tRNA molecules are shown in red.

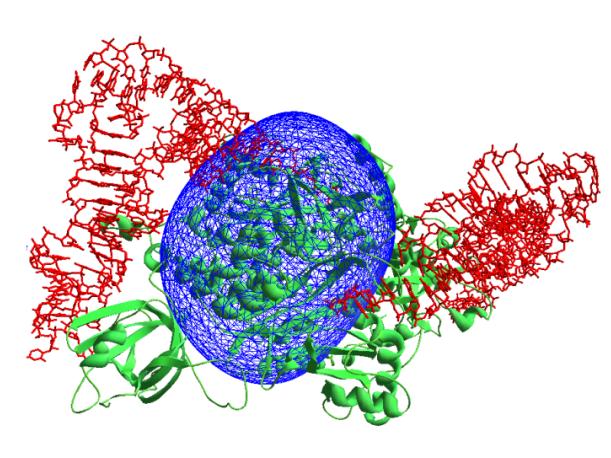
Fig. 3 Synthesis calculated at 45 Å resolution (37 reflections) using experimental modules corresponding to the protein molecules and phases obtained ab initio.

Protein molecule is shown in green and tRNA molecules are shown in red.