Atomic
displacement in incomplete models caused by optimisation of crystallographic
criteria
by
P.V.
Afonine
LCM3B, UMR 7036 CNRS, Université Henri Poincaré, Nancy 1, B.P. 239, Faculté
des Sciences, Vandoeuvre-lès-Nancy,
54506 France, and
Centre
Charles Hermite, LORIA, Villers-lès-Nancy, 54602 France
Abstract
It is known that
incompleteness of the atomic model can seriously affect its refinement. In
particularly, the minimisation of a crystallographic criterion (least-squares
or maximum-likelihood) shifts the atoms of an incomplete model from their exact
positions. The more incomplete model, the larger the mean atomic displacement.
This article studies individual atomic displacements in such a model.
Introduction
The basic goal of a crystallographic refinement is to obtain a model that is consistent as much as possible with the experimental diffraction data. For example, the conventional least-squares refinement fits structure factor modules calculated from the model to the experimental values. This goal is justified when one deals with a complete model which practically is never the case. Even at late stages of refinement some fragments with high B factors, some solvent molecules and often the bulk solvent are not taken into account. For such models, the structure factor magnitudes calculated from the exact model are different from observed amplitudes even in an ideal case without experimental errors. As a consequence, in the test case when initially the atoms of an incomplete model are placed correctly, the minimisation of the least-squares criterion without stereochemical restraints shifts them from their correct positions (Afonine et al, 2001; Lunin et al, 2002).
This negative
effect can be reduced if the maximum-likelihood approach is used (Pannu &
Read, 1996; Bricogne & Irwin, 1996; Murshudov et al., 1997; Adams et al.,
1997) which takes into account the absent part of the model statistically.
Nevertheless, even in this case the mean atomic displacement can be quite large (Lunin et al,
2002).
A series of tests was carried out in
order to study the distribution of an atomic displacement over the model.
Numerical tests
The tests were
carried out with CNS complex (Brünger et
al., 1998) using the structure of Fab fragment of monoclonal antibody (Fokine
et al., 2000). This molecule
crystallises in space group P212121 with the
unit cell parameters a = 72.24Å, b = 72.01Å, c = 86.99Å and one Fab molecule
per asymmetric unit. The full model includes 439 amino acid residues and 213
water molecules. The observed structure factors were simulated by the
corresponding values calculated from the complete exact model in order to
exclude experimental errors from the analysis. The standard least-squares
criterion LS was used in the tests.
The minimisation of this criterion was performed till the convergence
independently at the resolution dmin>2.2Å
(the resolution at which the model was constructed). For comparison, the second
series of tests was done at dmin>1.3Å.
Two incomplete starting models were generated by random deletion of
approximately 3 and 20 % of atoms, both macromolecular and water oxygens. In
all tests, the atoms of such incomplete models initially were placed at their
correct positions.
For each atom of
an incomplete model two distances were calculated:
1)
the distance between this atom in the starting model and the nearest removed
atom;
2)
a similar distance in the model after minimisation.
Results and discussion
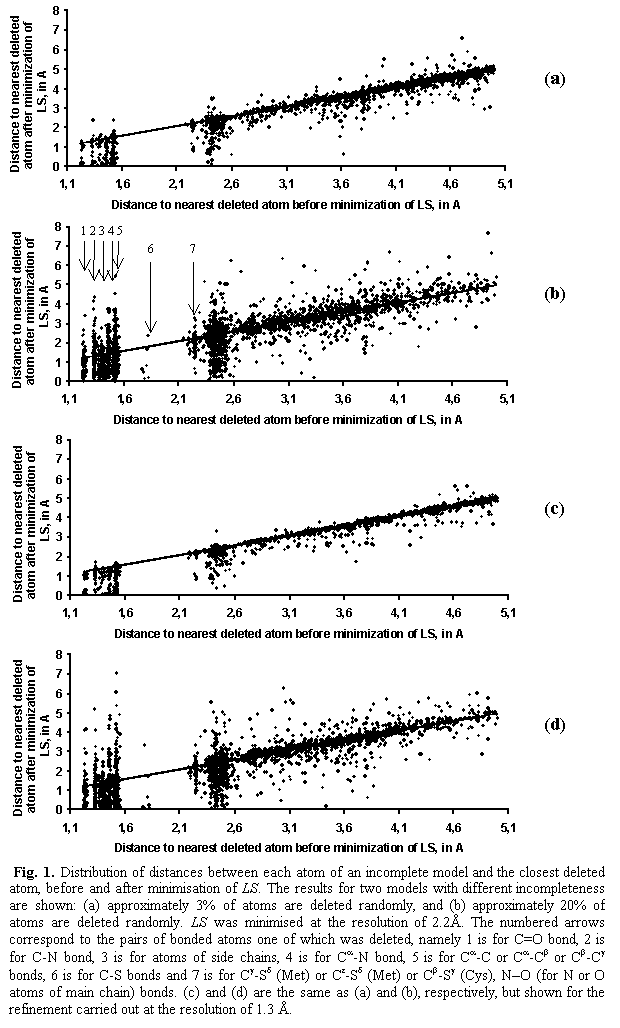
Fig. 1 shows the
distribution of distances between each atom of an incomplete model and the
former position of the closest deleted atom before and after minimisation of
the LS criterion. The maximal shift
corresponds to the atoms situated in the sphere of approximately 2.4 Å radius
around the deleted atom. These are atoms covalently bonded to it or located
within the van der Waals distance. Most of such atoms shift towards the
positions of deleted atoms (points below the straight diagonal line; final
distance is smaller that the initial distance). For the atoms situated far away
from the deleted atom, the shifts are much smaller and less regular, both to
and from the deleted atom.
The separated
bars at the left side of Fig. 1 correspond to specific pairs of bonded atoms
one of which was deleted. For example, the bar 1 corresponds to the double bond
atoms C=O where either C or O atom was deleted, the bar 2 is for the C–N bond,
etc. The bar 6 corresponds to the C–S bond.
In the case of
the 3%-incomplete model (Fig. 1a), the tendency of atoms to move toward the
place, previously occupied by a deleted atom, is seen much better in comparison
with the case of 20%-incomplete model (Fig 1b). A possible reason may be that
in the latter case it is more difficult to ‘choose’ the direction of its shift
because of a large number of ‘holes’ in the structure. It can be concluded that
the crystallographic criterion taken alone, without stereochemical restraints,
shifts the atoms of an incomplete model mostly toward the positions of deleted
atoms trying to compensate their absence. Stereochemical restraints when used
allow reduction of such a displacement by cancelling differently oriented
shifts from linked atoms.
In the second
series of tests, when the minimisation of the criterion was carried out at a
higher resolution of 1.3 Å, the behaviour of atoms of
the partial model was the same (Fig. 1c and 1d).
References
Adams, P.D., Pannu,
N.S., Read, R.J., & Brünger, A.T. (1997). Proc.Natl.Acad.Sci.USA., 94,
5018-5023.
Afonine, P., Lunin,
V.Y. & Urzhumtsev, A.G. (2001). CCP4
Newsletter on Protein Crystallography, 39,
52-56.
Bricogne, G. &
Irwin, J. (1996). Proceedings of the CCP4
Study Weekend, 85-92.
Brünger, A.T., Adams,
P.D., Clore, G.M., DeLabo, W.L., Gros, P., Grosse-Kunstleve, R.W., Jiang,
J.-S., Kuszewski, J., Nilges, M., Pannu, N.S., Read, R.J., Rice, L.M.,
Simonson, T. & Warren, G.L. (1998). Acta Cryst., D54,
905-921.
Fokine, A.V., Afonine,
P.V., Mikhailova, I.Yu., Tsygannik, I.N., Mareeva, T.Yu., Nesmeyanov, V.A.,
Pangborn, W., Li, N., Duax, W., Siszak, E., Pletnev, V.Z. (2000). Rus. J Bioorgan Chem, 26, 512-519.
Lunin, V.Y. &
Urzhumtsev, A. (1999). CCP4 Newsletter on
Protein Crystallography, 37,
14-28.
Lunin, V.Y., Afonine
P.V. & Urzhumtsev, A. (2002). Acta
Cryst. A58, 270-282.
Murshudov, G.N., Vagin, A.A. &
Dodson, E.J. (1997). Acta Cryst., D53, 240-255.
Pannu, N.S. &
Read, R.J. (1996). Acta Cryst., A52, 695-668.