Search
of the optimal strategy for refinement of atomic models
P. Afonine§,*, V.Y. Lunin#,* & A. Urzhumtsev*
$ Centre Charles Hermite, LORIA, Villers-lès-Nancy, 54602 France
# IMPB, Russian Academy of Sciences, Pushchino, 142290, Moscow Region,
Russia
* LCM3B, UPRESA 7036 CNRS, Université Henri Poincaré, Nancy 1, B.P. 239,
Faculté des Sciences, Vandoeuvre-lès-Nancy, 54506 France
e-mail: afonine@lcm3b.uhp-nancy.fr
1.
Introduction
Recently it has been shown (Afonine et al, 2001; Lunin et al., 2002)
that the approximation of the maximum likelihood criterion (ML) by a quadratic
functional (Lunin & Urzhumtsev, 1999) allows to understand the features of
the ML refinement and its advantages with respect to the traditional
least-squares (LS) refinement. In this latter, the magnitudes 
of structure factors
calculated from the current atomic model are fitted to the observed structure
factor magnitudes 
by minimisation of
, (1)
The weights
may reflect the accuracy of the observed magnitudes or some
other effects, but most frequently the unit weights are used.
In the procedure that
is usually referenced as ML-refinement the minimised criterion is the negative
logarithm of the likelihood, the model-dependent part of which may be presented
as
(2)
with
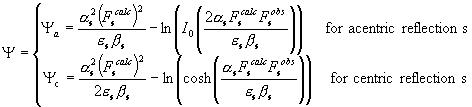. (3)
For every
reflection, its parameter 
depends on the reflection indexes and
particular space group and the statistical parameters 
and 
,
being the functions of the resolution, reflect the precision of the atomic
parameters and the completeness of the model (see for example Lunin &
Urzhumtsev, 1984; Read, 1986; Lunin & Skovoroda, 1997; Skovoroda &
Lunin, 2000).
The
approximation of the criterion (2,3) by a quadratic functional means its
substitution by a functional
. (4)
where the target values
are no longer the observed magnitudes and the non-unit
weights 
are crucial for a
successful refinement. The minimisation of this function we will call
LS*-refinement.
Previously (Lunin et
al., 2002) we have discussed that 
and 
in (4) may be
represented as
, 
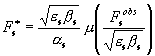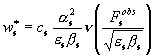, (5)
where m(p) and n(p) are some functions defined in Lunin et al. (2002) and whose behaviour
explains the features of the ML refinement.
Formula (5) shows that the parameters 
and 
, play the key role in the estimation of 
and 
and therefore in the
whole refinement. In this article we discuss the best choice of 
and 
.
2.
Estimation of 
and 
Several approaches can be suggested to
estimate the parameters 
and 
. If there exists some probabilistic hypothesis about
irremovable errors in the atomic model (for example, about a missing part of
the model) then for several particular cases these parameters may be calculated
explicitly (Urzhumtsev et al., 1996). In particular, in the case of an
incomplete model, if the absent atoms are supposed to be distributed uniformly
in the unit cell, these parameters may be calculated as
and 
, (6)
where fk(s) are
atomic scattering factors of the absent atoms. It should be noted that in
practice the exact number of missed atoms and their
scattering factors can be known only approximately (for example, it is
difficult to know the exact number of missed ordered solvent molecules).
Another
way is to use likelihood-based estimates of these parameters when comparing the
observed structure factor magnitudes with the ones corresponding to a starting
atomic model (Lunin & Urzhumtsev, 1984; Read, 1986). It is important to
note that the test set reflections (Brünger, 1992) only should be used (Lunin
& Skovoroda, 1995; Skovoroda & Lunin, 2000). Eventually, these estimates can be recalculated
iteratively during refinement.
These
different ways to estimate 
and 
have been tested by comparison of LS-, ML-
and various LS*-refinement approaches in order to suggest the best refinement
strategy.
3.
Models and programs used for tests
Similarly to the previous work (Afonine et al., 2001; Lunin et al., 2002), the tests were carried out with CNS complex (Brünger et al., 1998) using the model of Fab fragment of monoclonal antibody (Fokine et al., 2000) which consists of 439 amino acid residues and 213 water molecules, 3593 atoms in total. The crystal belongs to the space group P212121 with the unit cell parameters a = 72.24 Å, b = 72.01 Å, c = 86.99 Å, one molecule per asymmetric unit.
For test purposes the values of Fobs at 2.2 Å resolution were simulated by the corresponding values calculated from the complete exact model and were used for all refinements. The errors in the atomic co-ordinates were introduced randomly and independently. Incomplete models were obtained by random deletion of atoms, both from the macromolecule and from the solvent.
4.
Choice of 
and 
Several refinement strategies based on different
choice of 
and 
through different
estimation of 
and 
have been compared.
First of all, the parameters 
and 
have
been calculated using the technique described previously (Lunin &
Skovoroda, 1995; Skovoroda & Lunin, 2000) through the comparison of the 
magnitudes with the
structure factors 
calculated from the
starting model. These values were kept for the whole refinement process
consisted of 800 cycles.
Secondly, the same method of the estimation of 
and 
has
been applied but their values were recalculated every 400 or 200 refinement
cycles, depending on the test.
Alternatively, the refinement was carried out using
the estimations (6). In these tests the exact number of missed atoms and their
scattering factors were supposed to be known.
Finally, the refinement was carried out with the mixed
parameter values, 
= 1 for all reflection as in (6) and 
estimated from the comparison of 
with 
.
The start models with the mean coordinate errors of 0.5 and 0.7 Å respectively and with 0.5% and 3.0% of incompleteness were optimised using LS*-criterion (4). For comparison, corresponding LS- and ML-refinements were also done. The results of these tests are shown in Table 1. It can be remarked that, as it has been discussed (Afonine et al., 2001; Lunin et al., 2002), even a small quantity of absent atoms can already strongly influence on the quality of the refined model.
Table 1. Mean coordinate errors in the
model after refinement using different criteria. Starting models have mean
coordinate errors of Dst . The incompleteness Dabs of the models of 0.5% and 3.0% correspond to 18 and
108 atoms deleted, respectively. The number of cycles indicates the frequency
with which the parameters of the corresponding criterion were recalculated (the
frequency of parameters updating is not definitely known for ML). aF and bF stand for the parameters estimated from
the magnitude comparison and bC stands for values calculated from (6). The
final coordinate errors shown in italic indicate the cases where this error is
higher than the starting error. The numbers in bold indicate the best
refinement protocol for the given model.
|
criterion |
|
LS* aF,bF |
|
|
LS* a=1,bF |
|
LS* a=1,bC |
LS |
ML |
|
No of cycles |
1*800 |
2*400 |
4*200 |
1*800 |
2*400 |
4*200 |
1*800 |
1*800 |
800*1? |
|
Dst Dabs |
|
|
|
final |
error |
|
|
|
|
|
0.5Å 0.5% |
0.320 |
0.140 |
0.103 |
0.358 |
0.156 |
0.127 |
0.111 |
0.212 |
0.108 |
|
3.0% |
0.453 |
0.345 |
0.397 |
0.475 |
0.353 |
0.311 |
0.247 |
0.375 |
0.305 |
|
0.7Å 0.5% |
0.784 |
0.636 |
0.468 |
0.633 |
0.491 |
0.388 |
0.284 |
0.397 |
0.353 |
|
3.0% |
0.803 |
0.711 |
0.592 |
0.700 |
0.599 |
0.527 |
0.404 |
0.530 |
0.537 |
5. Influence of errors in
the estimation of 
The LS*-refinement with the
parameters estimated through (6) gives systematically better results in
comparison with other known strategies and was chosen as the best one for
further tests. The estimation of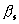 
in (6) depends on the number of
missed atoms, on their type and on their temperature factors. The influence of
possible errors in the estimation of these parameters from these 3 sources on
the results of refinement has been studied.
First of all, the missed atoms were
simulated by oxygens or by carbons with temperature factors as they were in the
corresponding deleted atoms. No significant influence of such modification of
the atomic type has been found (Table 2).
Table 2. Mean coordinate errors after LS*-refinement with the estimations (6) for different type assigned to missed atoms; CNO stands for the exact (mixed) type of atoms. Starting models have mean coordinate errors of Dst (in Å). Dabs is incompleteness of the models in percents; the number in parenthesis is the corresponding number of deleted atoms. The final coordinate errors shown in italic indicate the cases where this error is higher than the starting error.
|
Dst |
Dabs Type |
0.5
(18) |
1.0
(36) |
3.0
(108) |
5.0
(180) |
7.0 (252) |
9.0
(325) |
|
|
CNO |
0.105 |
0.133 |
0.256 |
0.343 |
0.447 |
0.513 |
|
0.5 Å |
O |
0.111 |
0.138 |
0.247 |
0.357 |
0.450 |
0.521 |
|
|
C |
0.113 |
0.136 |
0.256 |
0.343 |
0.439 |
0.499 |
|
|
CNO |
0.289 |
0.321 |
0.422 |
0.498 |
0.579 |
0.649 |
|
0.7 Å |
O |
0.284 |
0.278 |
0.404 |
0.468 |
0.598 |
0.645 |
|
|
C |
0.285 |
0.334 |
0.425 |
0.494 |
0.609 |
0.656 |
Table 3. Mean coordinate errors for different values <B> of the mean temperature factor assigned to missed atoms. Starting models have mean coordinate errors of Dst (in Å). Dabs is incompleteness of the models; the number in parenthesis is the corresponding number of deleted atoms. The final coordinate errors shown in italic indicate the cases where this error is higher than the starting error.
|
<B>,
Ų |
Dst Dabs= |
0.5
(18) |
1.0
(36) |
3.0
(108) |
5.0
(180) |
7.0
(252) |
9.0
(325) |
|
5 |
|
0.085 |
0.129 |
0.281 |
0.386 |
0.528 |
0.582 |
|
15 |
|
0.083 |
0.120 |
0.259 |
0.342 |
0.455 |
0.508 |
|
25 |
0.5 Å |
0.109 |
0.144 |
0.258 |
0.347 |
0.440 |
0.506 |
|
35 |
|
0.144 |
0.167 |
0.272 |
0.353 |
0.449 |
0.483 |
|
45 |
|
0.170 |
0.207 |
0.290 |
0.380 |
0.470 |
0.507 |
|
5 |
|
0.178 |
0.233 |
0.378 |
0.508 |
0.626 |
0.693 |
|
15 |
|
0.264 |
0.274 |
0.377 |
0.474 |
0.565 |
0.610 |
|
25 |
0.7 Å |
0.304 |
0.356 |
0.431 |
0.522 |
0.605 |
0.655 |
|
35 |
|
0.374 |
0.432 |
0.494 |
0.595 |
0.677 |
0.703 |
|
45 |
|
0.517 |
0.581 |
0.599 |
0.719 |
0.774 |
0.781 |
To study the influence of the estimated temperature
factor on the minimisation process, the known values of B-factors of missed
atoms (following the results of previous test, all these atoms were assigned to
be carbons) were considered to be equal to the same value which varied from 5
to 80 Å2 in a series of runs while the mean value of the temperature factor for
the deleted atoms varied in the limits 27-29 Å2. Table 3 shows that the variation of the
estimated temperature factors of missing atoms by ±15 Å2 around the mean values does not seriously affect the quality of the
refined model.
Finally, the influence of a wrong estimation of the
number of missed atoms has been studied. For this purpose the start model with
5.0% (180 atoms) of deleted atoms and introduced error of 0.5 Å was generated. Different estimations of the
number of missing atoms were used to get the 
values
and corresponding 
and 
. The error in this number of order of at least 25%
practically did not influence the final coordinate errors.
6.
Conclusions
The quadratic approximation of the maximum-likelihood-based criterion allows to understand better the features of the ML-based refinement and its advantages. Even more, this approximation allows to choose a better refinement strategy and to build its new quadratic functional the minimisation of which leads to better models that those obtained both by traditional LS and ML-based refinement.
In
this quadratic functional, the corresponding target values 
and the weights 
are calculated using
formulas (6) for the parameters 
and 
of the variable part of the likelihood function (2,3). These
formulas allow to get such estimation for the ideally refined model without
knowing directly its parameters and therefore to build the quadratic
approximation of (2,3) at the point of its minimum and thus to improve the
refinement criterion.
These
estimations of 
and 
are quite insensible to the choice of the type of atoms supposed
to be missed, to their mean B-factor estimation and to the estimation of the
number of such missed atoms making such new refinement strategy quite robust.
Acknowledgment
The work was
supported partially by RFBR grants 00-04-48175 and 01-07-90317, by CNRS, UHP
and Region Lorraine through financial support. The authors thank C. Lecomte and
E. Dodson for their interest to the project.
References
Afonine, P., Lunin,
V.Y. & Urzhumtsev, A.G. (2001). CCP4
Newsletter on Protein Crystallography, 39,
52-56.
Brünger, A.T. (1992). Nature, 355, 472-474.
Brünger, A.T., Adams,
P.D., Clore, G.M., DeLabo, W.L., Gros, P., Grosse-Kunstleve, R.W., Jiang,
J.-S., Kuszewski, J., Nilges, M., Pannu, N.S., Read, R.J., Rice, L.M.,
Simonson, T. & Warren, G.L. (1998) Acta
Cryst. D54, 905-921.
Fokine, A.V., Afonine, P.V., Mikhailova, I.Yu.,
Tsygannik, I.N., Mareeva, T.Yu., Nesmeyanov, V.A., Pangborn, W., Li, N., Duax,
W., Siszak, E., Pletnev, V.Z. (2000). Rus.
J. Bioorgan. Chem.,
26, 512-519.
Lunin, V.Y., Afonine, P.V., Urzhumtsev, A. (2002). Acta Cryst., A, in press.
Lunin, V.Y. &
Skovoroda, T.P. (1995). Acta Cryst.,
A51, 880-887.
Lunin, V.Y. & Urzhumtsev, A. (1984). Acta Cryst., A40, 269-277
Lunin, V.Y. &
Urzhumtsev, A. (1999). CCP4 Newsletter on
Protein Crystallography, 37,
14-28.
Skovoroda, T.P. & Lunin, V.Y. (2000).
Crystallography Reports 45, part. 2, 195-198.
Urzhumtsev, A.G., Skovoroda, T.P. & Lunin,
V.Y (1996). J.Appl.Cryst., 29,
741-744.