Bulk solvent correction for yet unsolved structures

  

By A. Fokine & A. Urzhumtsev

 

Laboratory of Crystallography and Modelling of Mineral and Biological Materials, UPRESA 7036 CNRS, University Henri Poincaré, Nancy I, 54506 Vandoeuvre-lès-Nancy, France

e-mail : fokine@lcm3b.uhp-nancy.fr

 

 

 

Abstract

 

The bulk solvent correction becomes a routine tool for macromolecular structure determination because the low resolution diffraction data contain an important structural information but cannot be used without such correction. The most reliable of the existing solvent correction methods is the flat solvent model. However, this method can be applied only when an atomic model is already placed in the unit cell; this is necessary in order to estimate two key parameters of the bulk solvent model, k_sol and B_sol . The statistical analysis of values of these parameters for already resolved structures shows that their fluctuation is relatively weak; as a rule the outliers correspond to incorrectly determined parameters. Therefore, the mean values of k_sol = 0.35 e/ų and B_sol = 46 Ų may be used when refined values cannot be obtained thus extending essentially the limits of the application of the flat bulk solvent model. In particular, such modelling allows to increase drastically the signal in the translation search in molecular replacement.

 

 

1. Introduction

The macromolecular crystals contain a large part of disordered (bulk) solvent whose contribution to low resolution reflections is quite significant. An atomic model of a macromolecule without the contribution of the bulk solvent cannot describe these low-resolution diffraction data correctly. On another hand, these data are important to avoid map distortion (Podjarny et al., 1981; Urzhumtsev, 1991) and to refine efficiently and correctly the atomic macromolecular model (Kostrewa, 1997). It can be thought also that these data can greatly improve the resolution of the translation problem in Molecular Replacement (MR) method because they are insensitive to reasonable errors in the atomic positions and in the model orientation.

Among several methods allowing to estimate structure factors of the bulk solvent (for a review see Jiang & Brünger 1994; Badger 1997), the flat solvent model (Phillips, 1980; Jiang & Brünger 1994) has been proven to be of a superior quality with respect to others (Jiang & Brünger 1994; Kostrewa, 1997).

In this model the binary function M (solvent mask) is introduced which is equal to 1 inside the solvent region and to 0 outside. The structure factors of the bulk solvent are calculated as the scaled Fourier transform ℱ of this function :

F_solv(k_sol,B_sol) = k_sol  exp(-B_solsin²(q)/l²) ℱ(M)                                                    (1)

The unknown parameters k_sol and B_sol of the bulk solvent are chosen from the best fit of total calculated structure factor F_total  to experimental data :

 

G(k_sol,B_sol) = S [ |F_obs| - |F_solv(k_sol,B_sol) + F_atoms | ] ²  à min                                 (2)

 

where F_atoms are the structure factors calculated from the ordered atoms. Therefore, the knowledge of an atomic model of macromolecule already placed in the crystal is necessary to estimate k_sol and B_sol , the key parameters of the method.

 

 

2. Statistical analysis of the bulk solvent parameters

 

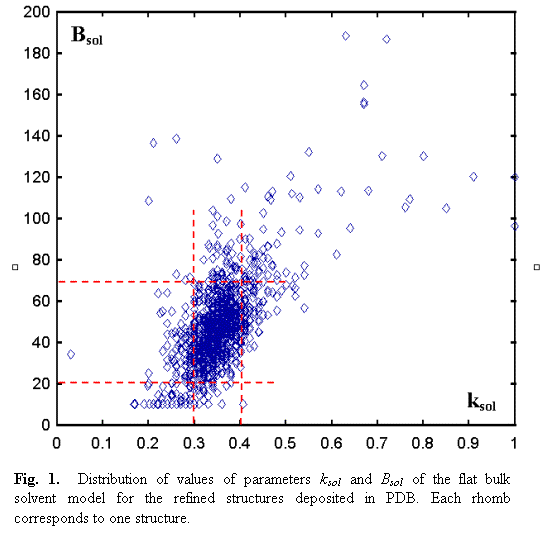
In order to study the variability of the values of k_sol and B_sol we analysed their distribution for the structures deposited in the Protein Data Bank (Bernstein et al., 1977). The corresponding models have been selected using the provided software (3DB Browser; http://pdb-browsers.ebi.ac.uk/pdb-bin/pdbmain). The obtained distribution (Fig. 1) shows that for the most of structures the parameter k_sol varies between 0.3 and 0.4  e/ų and B_sol varies between 20 and 70 Ų. The mean values are equal to  = 0.35 e/ų and  = 46 Ų, and the dispersion are 0.03 e/ų and 17 Ų , respectively (this statistic was calculated for the models with 0< k_sol <0.6 e/ų and 0< B_sol <100 Ų).

A detailed study has been carried out for some outliers with the experimental data available in PDB in order to find the reason for such unusual values of the scale parameters. In all cases the deposited parameters have been found to be incorrect, and the optimal values obtained by us with the complete data set using the systematic search were in the limits reported above.

For such small variation of the scale parameters, the corresponding variation of the structure factors F_solv(k_sol,B_sol) is also relatively weak suggesting that the mean values  and  can be used when the refined values of the parameters can not be obtained. In particular, they can be used for the molecular replacement when low resolution data are used as it is discussed below. Another application is a map improvement when only a molecular envelope is known (Fokine & Urzhumtsev, 2001).

It should be noted that the distribution of k_sol and B_sol is quite different from that obtained for similar parameters of the exponential scaling model (Glykos & Kokkinidis, 2000). This can be explained by a more poor quality of this latter model, specially at a middle resolution (Urzhumtsev & Podjarny, 1995a), and by less clear physical meaning of the parameters of the exponential model.

 

 

3. Bulk solvent correction and fast translation search

It has been shown by Urzhumtsev & Podjarny (1995b) that low resolution reflections being less sensitive to model imperfection (including the errors in its orientation) can be extremely useful for the solution of the translation problem. However, standard molecular replacement protocols, except those by Glykos & Kokkinidis (2001) where the exponential model is used, do not use reflections with the resolution lower than 10-15 Å because they are strongly influenced by the bulk solvent.

For the translation search, the bulk solvent correction eventually can be done at every position of the search model (while the obtained k_sol and B_sol can be completely unreasonable for wrong positions). Unfortunately, such way of solvent correction cannot be included into fast translation algorithms (Navaza, 1994; Navaza & Vernoslova, 1995) making its practical application inefficient. However, the following observations can be done :

a)      For the positions in the unit cell where the search model does not overlap with its symmetrically related copies, the mask of the region occupied by all molecules can be calculated as a junction of masks of individual molecules related by symmetries; as a consequence, the structure factors of such total molecular envelope can be rapidly recalculated from the structure factors of the envelope of a single model;

b)      if the structure factors of the envelope of a single model are preliminary scaled by  and , such total structure factors summarised over the symmetries give a good estimation of the bulk solvent structure factors;

c)      for all non-overlapping model positions, such scaled structure factors from the envelope being added to the structure factors from the atomic model and expanded over all symmetries are structure factors from the whole content of the unit cell;

d)      as a conclusion, a fast FFT-based translation search (Navaza, 1994; Navaza & Vernoslova, 1995) done using bulk-solvent-corrected structure factors instead of the values calculated directly from the atomic model allows to compare correctly the magnitudes of all reflections including those at low resolution for all non-overlapping positions.

 

Naturally, spurious peaks in the translation function are eventually possible for the positions where the models overlap; however, these spurious peaks will be eliminated by the packing criterion and will not appear in the final list anyhow.

 

 

4. Tests protocols

 

A good approximation for the molecular envelope can be available from a more or less complete atomic model. This is the case when NMR models are used as the search models for the molecular replacement. Several such cases reported as most difficult (for a corresponding review see Chen et al., 2000; Chen, 2001) were chosen to test the suggested approach of the improvement of the translation function (Table 1).

All test calculations were done with experimental data, and the orientation of the search models was supposed to be known (it can be noted that typical errors of about 5° in model orientation practically did not influence the searches when low resolution reflections were included). All translation searches were made with CNS (Brünger et al., 1998) using the fast translation function (Navaza & Vernoslova, 1995). The translation search parameters were taken without any optimisation (Chen at al., 2000); complete NMR models were taken as they are in the PDB; the B-factors for all atoms of the search models were assigned to be equal to 20 Ų. In each test, a single NMR model was used for the translation search.

 

Table 1.  Test structures : summary information

 

Protein name (reference)	PDB ID / NMR ID	Space group and unit cell parameters a,b,c (in Å)	Percentage of the solvent in the unit cell
Human interleukin-4 (Müller et al.,1995)	1hik 1bcn	P41212 92.1, 92.1, 46.4	63
P53 Tetramerization Domain (Mittl et al., 1998)	1aie 1pet	P422 45.5, 45.5, 32.2	53
Corn Hageman Factor Inhibitor (Behnke et al. 1998)	1bea 1bip	P42212 57.12, 57.12, 80.24	49

 

 

 

 

5. Results of improved translation searches

 

Figure 2 shows the results of the translation searches performed with and without low resolution data, with and without the bulk solvent correction using three experimental data sets. Each diagram shows the results of the translation search at a given resolution shell. The top diagrams show the peaks obtained in the translation search without any bulk solvent correction; the down diagrams show the peaks obtained at the same conditions when the bulk solvent correction was taken into account as suggested above. The height of each peak is shown in percents to the height of the first peak of the corresponding search, and the correct solution is indicated in red. It may be reminded that the total computation time for both type of the translation function was the same due to the fast correction procedure described in the previous section.

For human interleukin-4 (Müller et al., 1995), the translation search performed at the standard resolution of 4-15 Å without solvent correction gave the solution as the second peak. Including of all available reflections with the resolution lower than 15 Å brought the correct peak to the first position. Bulk solvent correction increased the contrast of the signal drastically, specially when low resolution data were included (Fig. 2a).

For p53 tetramerization domain (Mittl et al., 1998), the translation search without solvent correction at standard 4-15 Å resolution gave the correct solution hidden in noise and the search at 3-15 Å resolution gave it slightly higher in the list. With the solvent correction, the peak for the solution became the first with the best contrast at 4 Å even when no more low resolution data are available (Fig. 2b).

CHFI (Behnke et al., 1998) was reported as the worst case among all NMR-based searches (Chen et al., 2001). The multiple rotation function (Urzhumtseva & Urzhumtsev, 2001) allowed to find the orientation of the search model quite unambiguously and precisely and it was supposed to be known for the translation search. Without the bulk solvent correction, the solution did not appear among 10 highest peaks neither at the resolution 5-15 Å nor at 4-15 Å. When all available magnitudes with the resolution lower than 5 Å were used, the correct peak was the 7^th in height. At the same time, with the bulk solvent correction, this peak became the first one for the resolution lower than 5 Å while the contrast is not so high as for two previous cases (Fig. 2c).

Therefore, it can be concluded that the bulk solvent correction using the flat solvent model improves drastically the translation function, quite differently from the correction by the exponential model where no significant improvement has been observed (Glykos & Kokkinidis, 2001).

 

 

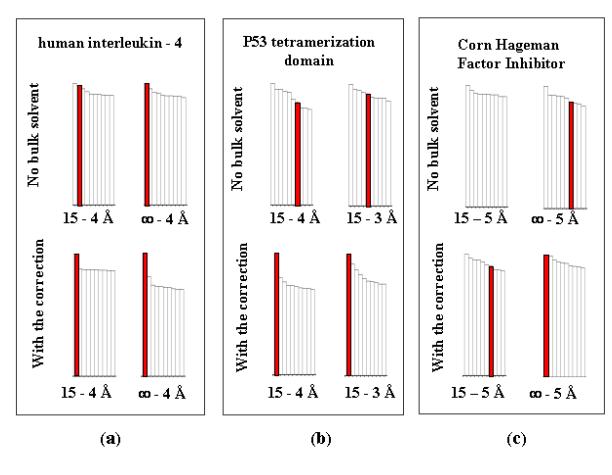
Fig. 2  Relative heights of peaks of the translation function Each column represents a peak of the translation function and has a height in percents to the value of the first (highest) peak obtained at the same translation search. For each resolution range ten highest peaks corresponding to searches without solvent correction are shown at the  top diagram and ten highest peaks corresponding to searches with such correction are shown at the bottom diagram. Peaks corresponding to the correct solution are shown in red. The figures represent the results of the searches for : a)      human interleukin-4 (Müller et al., 1995), b)      p53 tetramerization domain (Mittl et al., 1998), c)      Corn Hageman Factor Inhibitor (Behnke et al., 1998).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6. Physical meaning and possible values of the parameters of the flat solvent model

 

It has been discussed many times, that the parameter k_sol describes the mean electron density of crystallisation solution. Kostrewa indicated (1997) that the electron density of pure water is 0.33 e/ų, the density of  4M ammonium sulphate is 0.41 e/ų, so normally the value of k_sol should vary between these limits which corresponds well to the distribution found from the PDB analysis (Section 2).

It is clear that the parameter B_sol describes the sharpness of the solvent density at its border but his physical meaning has not been discussed previously. The larger is B_sol the deeper the electron density of the solvent penetrates to the macromolecular region and therefore very large values of B_sol are meaningless. On the other hand, the distance interval on which the electron density of the solvent decreases to zero should be at least larger than the radius of the solvent molecule (1.4 Å).

In fact, we have found that the optimal value of this parameter corresponds to the mostly flat electron density distribution at the border between the solvent and molecular regions (details will be published elsewhere; manuscript in preparation). Again, these values agree well with the distribution found statistically.

It can be noted that a non optimal choice of parameters does not allow to fit equally well all calculated data to the experimental values and usually leaves elevated R-factor for lowest resolution reflections. In most of cases, such wrong choice can be avoided either by a systematic search or by a local search for k_sol and B_sol as it is realised in CNS (Brünger et al., 1998) but starting from  and , differently from the currently existing procedure.

 

 

 

7. Conclusions

 

The distribution of values of the bulk solvent parameters k_sol and B_sol for crystallographic structures deposited in Protein Data Bank shows that their correct values vary in relatively small limits around  = 0.35 e/ų and = 46 Ų. These limits and corresponding mean values have a reasonable physical interpretation; k_sol corresponds to the means electron density of the solvent and the optimal value of B_sol provides with the smooth and flat transition of the electron density between the solvent and molecular regions.

For a known atomic model in the unit cell, the optimal values of the bulk solvent parameters can be found either by systematic or by a local search; in the latter case, the start from  and  allows to avoid a wrong answer.

When the standard procedure can not be applied to obtain the optimal values of the parameters, for example when an atomic model in the unit cell is not known yet, the mean values  and  can be used instead of the optimal values.

In particular, this latter allows to include the bulk solvent correction using the flat solvent model into fast calculation of the translation function. The use of low resolution reflections with such bulk solvent correction improves drastically the signal in the translation search.

 

 

 

References 

 

Badger, J. (1997). Methods Enzymology. 277, 344-352.

Behnke, C.A., Yee, V.C., Le Trong, I., Pedersen, L.C., Stenkamp, R.E., Kim, S.-S.,

    Reeck, G.R. & Teller, D.C. (1998). Biochemistry, 37, 15277-15288.

Bernstein, F. C., Koetzle, T. F., Williams, G. J., Meyer, E. E. Jr., Brice, M. D., Rodgers, J. R., 

    Kennard, O., Shimanouchi, T. & Tasumi, M. (1977). J. Mol. Biol. 112, 535-542.

Brünger, A.T., Adams, P. D., Clore, G. M., DeLano, W. L., Gros, P., Grosse-Kunstleve, R. W., 

    Jiang, J.-S., Kuszewski, J., Nilges, M., Pannu, N. S., Read, R. J., Rice, L. M., Simonson, T.

    & Warren, G. L. (1998). Acta Cryst., D54, 905-921.

Chen, Y.W., Dodson, E.J. & Kleywegt, G.J. (2000). Structure, 8, 213-220.

Chen, Y.W., (2001). Acta Cryst. D57, 1457-1461.    

Fokine, A. & Urzhumtsev, A. (2001). CCP4  Newslett. 39, 71-78.

Glykos, N. M. & Kokkinidis, M. (2000). Acta Cryst. D56, 1070-1072.

Glykos, N. M. & Kokkinidis, M. (2001). Acta Cryst. D57, 1462-1473    

Jiang, J.-S. & Brünger, A. T. (1994). J. Mol. Biol. 243, 100-115.

Kostrewa, D. (1997). CCP4  Newslett. 34, 9-22.

Mittl, P., Chène, P. & Grütter, M.G. (1998). Acta Cryst. D54, 86-89.

Müller, T., Oehlenschläger, F. & Buehner, M. (1995) J.Mol.Biol., 247, 360-372.

Navaza, J. (1994). Acta Cryst. A50, 157-163.

Navaza, J. & Vernoslova, E. (1995). Acta Cryst., A51, 445-449.

Phillips, S. E. V. (1980). J.Mol.Biol., 142, 531-554.

Podjarny, A. D., Schevitz, R. W. & Sigler, P. B. (1981). Acta Cryst. A37, 662-668.

Urzhumtsev, A. G. (1991). Acta Cryst. A47, 794-801.

Urzhumtsev, A.G. & Podjarny, A.D. (1995a) CCP4 Newslett. 31, 12-16.

Urzhumtsev, A.G., Podjarny, A.D. (1995b) Acta Cryst., D51, 888-895

Urzhumtseva, L. & Urzhumtsev, A.G. (2001) CCP4 Newslett. 39,79-85