Binary Integer Programming and its Use for Envelope Determination

 

By

 

Vladimir Y. Lunin^1,2, Alexandre Urzhumtsev^3,† & Alexander Bockmayr²

 

¹ Institute of Mathematical Problems of Biology, Russian Academy of Sciences, Pushchino, Moscow Region, 140292 Russia

 

² LORIA, UMR 7503, Faculté des Sciences, Université Henri Poincaré, Nancy I, 54506 Vandoeuvre-les-Nancy, France; bockmayr@loria.fr

 

³ LCM3B, UMR 7036 CNRS, Faculté des Sciences, Université Henri Poincaré, Nancy I, 54506 Vandoeuvre-les-Nancy, France; sacha@lcm3b.uhp-nancy.fr

 

† to whom correspondence must be sent

 

 

Abstract

 

The density values are linked to the observed magnitudes and unknown phases by a system of non-linear equations. When the object of search is a binary envelope rather than a continuous function of the electron density distribution, these equations can be replaced by a system of linear inequalities with respect to binary unknowns and powerful tools of integer linear programming may be applied to solve the phase problem. This novel approach was tested with calculated and experimental data for a known protein structure.

 

 

1. Introduction

 

            Binary Integer Programming (BIP in what follows) is an approach to solve a system of linear inequalities in binary unknowns (0 or 1 in what follows). Integer programming has been studied in mathematics, computer science, and operations research for more than 40 years (see for example Johnson et al., 2000 and Bockmayr & Kasper, 1998, for a review). It has been successfully applied to solve a huge number of large-scale combinatorial problems. The general form of an integer linear programming problem is

                        max { c^Tx | Ax ≤ b, x  Zⁿ }                                                                           (1.1)

with a real matrix A of a dimension m by n, and vectors c  Rⁿ, b  R^m, c^Tx being the scalar product of the vectors c and x. If the system Ax ≤ b includes the constraints 0 ≤ x ≤ 1, we get a binary integer linear programming problem (BIP). A vector x* in Zⁿ with Ax* ≤ b is called a feasible solution. If moreover, c^Tx* = max { c^Tx | Ax ≤ b, x  Zⁿ }, then x* is called an optimal solution and c^Tx* the optimal value.

In our phasing technique, we have developed an approach that combines a general strategy of low resolution phasing developed recently by (Lunin et al., 2000) with a local search procedure for the solution of BIP problems (Walser, 1997, 1998). The general strategy suggests to generate a large number of phase sets and to filter them by some criterion in order to select a relatively small portion of probable solutions. While some of the probable solutions can be quite wrong, the ensemble of the selected phases set is, as a rule, mostly populated by the phase sets which are close enough to the correct solution. Therefore averaging the probable solutions gives a phase set of a high quality. The major problems of this approach are to identify a good selection criterion and to propose an efficient and fast search strategy. The efficiency of the search may be increased if some local refinement is applied to the generated random sets. The local search procedure realised in the program WSATOIP (Walser, 1997, 1998) allows one to perform this refinement when working with binary integer programming problems. The procedure begins the search with some randomly generated start values for the binary unknowns and then tries to improve the solution locally. In general, the optimisation does not result in the exact solution but in an ‘improved’ one, compared to the starting point.

 

 

2. Binary integer programming and crystallographic objects

 

                Crystallographic problems are usually formulated either in terms of real electron density values or in terms of complex structure factors. These two sets of variables are linked by a linear transformation (Fourier Transform) if the electron density values in all points of the unit cell and the full (infinite) set of structure factors are considered. In practice, when the density is calculated in a grid with a relatively small number of divisions along the unit cell axes, and a small number of reflections is used, these formulae need to be corrected. A possible way to introduce these corrections is to replace the equalities which link density values and structure factors by linear inequalities.

Additionally, the magnitudes of these complex structure factors are supposed to be known from the experiment while the phases are the subject of search. This introduces non-linearity into the problem. Nevertheless, for centric reflections where the phase may take only one of two possible values, phase uncertainty may be represented by a binary variable. The equations that link this variable and the electron density values with the magnitudes are still linear. In order to get a similar situation for acentric reflections, an approximation can be used. The phase of the corresponding structure factors is restricted to one of four possible values ,  instead of an arbitrary value between 0 and 2p ; this allows one to code the phase uncertainty by two additional binary variables, which are linked also linearly to the density values.

As a rule, macromolecular crystallographers do not need the exact density values but the position and the shape of the region where the density values lie above a certain level, i.e., a binary function representing this region : the molecular envelope, the trace of the polypeptide chain etc. Replacing the object of search by a binary mask has two important consequences. On the one hand, the restriction of the density values to 0 or 1 may enormously reduce the number of possible solutions of the phase problem. On the other hand, the equations connecting the search density values with the experimental structure factors are no longer strictly valid and require a correction.

 

 

3. Grid density function and grid structure factors

 

            Let   be the number of divisions along the unit cell axes (supposed to be consistent with the symmetry). Let  stand for the diagonal matrix with the diagonal formed by , P is the set of all grid points in the unit cell and  is the total number of these points:

.     (3.1)

We introduce the grid electron density function  as the set of values of the density distribution at the grid points:

,             ,                                                 (3.2)

and define the grid structure factors by the Inverse Discrete Fourier Transform (IDFT):

            ,          .                                                            (3.3)

The Discrete Fourier Transform (DFT) may restore the grid density function unambiguously from the grid structure factors:

            ,           ,                                                 (3.4)

but the values of the density distribution in the intermediate points cannot be retrieved. These grid structure factors are linked with the usual structure factors

      , .                                                          (3.5)

by the formula (Ten Eyck, 1973):

 

      .                                                                       (3.6)

If a Fourier synthesis of a finite resolution d_min is calculated at a grid whose step length is less than d_min/2, then all structure factors in the sum on the right-hand side of (3.6) are supposed to be zero.

 

4. The phase problem as a binary programming problem

 

            The main goal of this section is to derive linear inequalities that allow one to define the grid electron density values  provided the structure factor magnitudes  are known. Using formulae (3.3) and (3.6), one can write down a system of linear equations defining the values of the grid function  in the form

                    (4.1)

where

             .

These equations link the unknown grid density values linearly with the real and imaginary parts,  and , of the structure factors (if both the magnitudes and phases are supposed to be known). However, if not only the density values but also the phases are considered to be unknown, then the equations become non-linear because the phases enter as an argument of trigonometric functions.

The value of , which depends on magnitudes and phases of all structure factors is generally unknown.  Therefore, the equations (4.1) cannot be written in the precise form. In general, the expression  cannot be neglected if one of the indices is close to M₁/2, M₂/2, M₃/2. At the same time, it can be estimated by the sum of the structure factor magnitudes in the following way:

              .                                                                                    (4.2)

As a consequence, the equations (4.1) may be replaced by a system of inequalities that restrict the density values in a weaker form, but do not require the knowledge of all structure factors

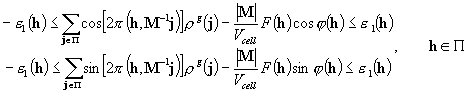   .                       (4.3)

            The inequalities (4.3) contain the phase values  which cannot be determined directly in an X-ray experiment and which are the object of our search. The phases enter the inequalities in a non-linear manner. However, if the reflection h is centric then only two values of the phase,  or , with  being known, are possible, and (4.3) may be written as

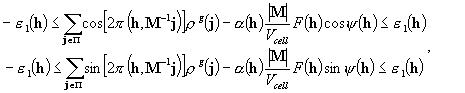for centric h,         (4.4)

Here, the phase ambiguity is represented by a new unknown , which takes one of the two values 1 or –1 and which enters the inequalities in a linear way. The inequalities (4.4) become linear with respect to  and  provided the structure factor magnitudes  are known.

For acentric reflections, an approximation can be done such that the phase  can take only one of four values: , . Under this hypothesis, the inequalities (4.3) become

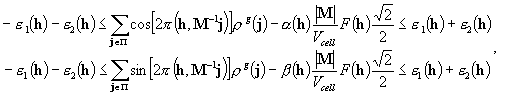for acentric h

            (4.5)

where the unknowns  and  take one of the two values 1 or –1, and enter the inequalities in a linear way. Here,  reflects the error introduced by the sampling of the phase value and can be estimated by

.                                                                                  (4.6)

As a result we get a system of linear inequalities (4.5) where the unknowns are the values of the electron density at the grid points , and where the additional variables  and  represent the phase ambiguity. These inequalities are weaker than the initial equations, but they reduce the phase problem to linear integer programming, while initially the phase problem is essentially non-linear. 

 

5.  Solution of the BIP phase problem

 

            One of the main difficulties in representing the phase problem as a BIP problem is that the X-ray experiment provides magnitudes  corresponding to a real electron density and not to a binary function approximating it. Nevertheless, tests show that (see Section 6.1), at low and middle resolution, the correlation between the observed structure factor magnitudes and those calculated from binary envelopes may be high enough even for coarse grids. The inequalities may now be written as

 

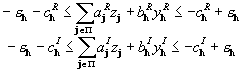,          ,                                                (5.1)

 

where ,  are unknown binary variables, which take 0 or 1 values only;

  ,                       (5.2)

         ,                                               (5.3)

,     for the centric case,                   (5.4)

,     for the acentric case,                             (5.5)

,         for the centric case,                   (5.6)

,           for the acentric case.                             (5.7)

 is the optimal scale factor which reduces the observed magnitudes to a ‘binary function scale’, and the gap  reflects three kinds of errors, namely grid sampling errors , phase sampling errors , and errors due to replacing the real density distribution by a binary function.

            It should be noted that in space groups different from P1 some variables are linked by the crystallographic symmetry and therefore a set of independent variables must be chosen before solving the system (5.1).

In our tests to solve the phase problem, we used an approach that combines local search for the solution of BIP problems (Walser, 1997, 1998) with a general strategy of low resolution phasing developed recently by (Lunin et al., 2000). First, a set of random initial assignments of values to the binary variables is generated. From every initial assignment, one tries to find a feasible solution of (5.1) by local flips of the binary variables. This is done by  the procedure WSATOIP (Walser, 1997, 1998). At each run, the program will try to minimise a residual, which is defined on the base of (5.1) as

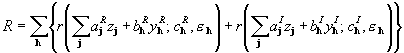       .                       (5.8)

Here

 

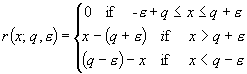                                                                      (5.9)

 

so that  if the inequality  is satisfied, and  grows linearly with x otherwise (see Fig.1). The program stops if the residual has been reduced to 0 (i.e. a feasible solution has been found) or if a given maximal number of flips  has been reached. So the result of a particular run is not always a feasible solution, but a final assignment where the initial residue has been reduced.

            For every final assignment, the phases corresponding to the binary function  are calculated and used together with the observed magnitudes to obtain Fourier syntheses. It must be noted that the possible phase solutions found by this procedure may correspond to different choices of the origin and enantiomer. Therefore, the calculated syntheses are first aligned according to permitted origin and enantiomer choices (Lunin & Lunina, 1996). Then they are averaged to produce a single phase set. In this, way a centroid phase value and an individual figure of merit are defined for every reflection (Lunin et al., 2000).

 

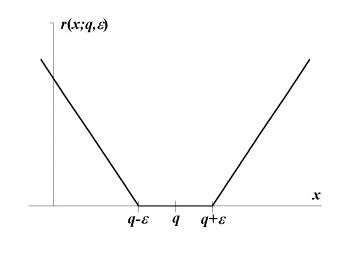
Fig.1. The penalty function used for the solution of BIP problem.

 

6. Computer tests

 

            The tests were performed with the Protein G data (Derrick & Wigley, 1984). This small protein (61 residues) contains one a-helix and one b-sheet. The protein was crystallised in the space group P2₁2₁2₁ with the unit cell dimensions 34.9×40.3×42.2 Å. The complete low resolution set of experimental diffraction magnitudes was available. The phases calculated from the refined atomic model were considered as the exact ones. The binary density was calculated at the grid N_grid x N_grid x N_grid with N_var independent density variables. In all phasing tests, N_runs starting randomly generated phases sets were optimised by WSATOIP, N_flips flips of binary variables were allowed for every of these runs. Some of the runs (N_R=0) converged to a set of variables giving the zero value of the criterion R. In any case, all results of the minimisation were analysed by a clustering procedure, giving each time a small number N_clust of phase clusters; one of these clusters (composed from N_solut phase sets) always corresponded to the correct solution of the problem. The calculations were done on a Pentium III / 500 PC.

 

6.1. Binary approximations of Fourier syntheses

 

            The goal of the first series of tests was to check how well small-grid binary functions approximate magnitudes and phases of structure factors. To get a binary approximation for the chosen grid, the Fourier synthesis  was calculated using the observed magnitudes and the exact phases. The binary approximation values  were set to 1 (molecular envelope) for the given number K of points with highest synthesis values, and to 0 otherwise. The quality of the approximation depends on this parameter K and special tests were performed to determine the optimal K values for different grids. It was found that the optimal ratio of the value K to the full number of grid points (the one which maximises the correlation) depends on the synthesis resolution and decreases when the resolution increases (Table 1). The grid structure factors  were then calculated and their magnitudes and phases were compared to the true ones (Table 1). This test demonstrated that even at surprisingly small grids, a binary envelope may provide low-resolution phases of a reasonable quality.

 

Table 1. Approximation of the observed structure factors by values calculated from binary maps

 

The correlation coefficients

and

are represented for different resolution zones. The molecular volume defines the number K of non-zero grid values. It was adapted for every grid to get the maximal correlation coefficient.

 

Grid (K = mol.vol., %)	CF / Cf : Resolution range (Å)   (Number of independent reflections)
	16-∞  (15)	12-∞  (28)	8-∞  (85)	5-∞ (305)	4-∞ (580)
6*6*6  (50)	0.32 / 0.93	0.39 / 0.74	-	-	-
8*8*8  (35)	0.88 / 0.98	0.92 / 0.94	0.0 / 0.80	-	-
10*10*10  (30)	0.68 / 0.98	0.73 / 0.96	0.68 / 0.90	-	-
16*16*16  (20)	0.91 / 0.99	0.79 / 0.99	0.69 / 0.94	0.62 / 0.87	0.03 / 0.81

 

6.2. Resolving the phase ambiguity for binary functions

 

            The goal of this test was to study to what extent the condition ‘0 or 1’ allows one to reduce the phase ambiguity. An idealised situation was considered, where the exact magnitudes of the real and imaginary parts of the binary structure factors

 ,   ,                                           (6.1)

were supposed to be known. In this case, the grid values satisfy the equations

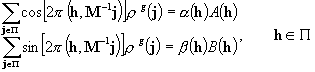                                                     (6.2)

where the unknowns  and  take one of the values 1 or -1.

            The equations (6.2) have a unique solution for any choice of right-hand side values (given by the Fourier transform of these values). So if the grid function is allowed to take any real values, the known magnitudes  do not define the solution uniquely. Any permutation of the signs of  and  will result in a solution of (6.2) possessing the same magnitudes . It may be expected that this is not the case if binary restrictions are added for the unknowns :

              .                                                                                                        (6.3)

Now an arbitrary choice of the signs of  and  may result in a solution of (6.2) which does not satisfy the condition (6.3). So the binary restrictions may reduce significantly the freedom of choosing the signs and thus may solve the phase problem (or, at least, reduce the phase ambiguity).

Table 2 shows the results of the corresponding tests. It can be noted that in all cases the procedure managed to get the correct solution. For the smallest grid this solution has characteristics similar to those of another, false phase set. Note also the computational difficulties for the largest tested grid .

 

Table 2. Test results for the resolution of the phase problem

 

Tests 1-3 were done with known magnitudes of the real and imaginary parts of the structure factors; tests 4-5  were done with known magnitudes of the structure factors, calculated from binary envelopes. For the notation of the columns, see Section 6.

 

Test N°	Ngrid	Nvar	% of  '1'	Nflips	CPU/run	Nruns	NR=0	Nsolut	Nclust
1	6	108	50	50,000	2 min	100	73	37	2
2	8	128	35	250,000	30 min	100	80	80	1
3	10	250	30	10,000,000	70 hrs	5	3	3	1
4	6	108	50	50,000	2 min	100	0	47	2
5	8	128	35	250,000	30 min	100	0	19	1

 

7.3. Known magnitudes for binary envelopes

           

            In a more realistic situation, the estimates (6.1) may be available for centric reflections only. For acentric reflections, only the value  of the magnitude of the complex structure factor may be assumed to be known. The goal of the next test series was to study how such uncertainty affects the solution. It was supposed in these tests that the magnitudes  of the binary structure factors are known exactly, while the magnitudes of their real and imaginary parts were estimated by

 ,  .                                                     (6.4)

A ‘gap’ was introduced into the equations (6.2) to take into account the errors caused by this approximation

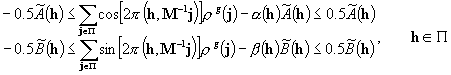       .           (6.5)

Due to these approximations, we cannot expect any longer that the true solution will satisfy (6.5), so the goal was to make the residual value (3.1) as small as possible.      

            The results of the numerical tests are presented in Table 2 (tests 4 and 5). In test 4, the cluster for the correct solution was slightly smaller (47 phase sets) than the second cluster (49 sets) corresponding to a false phase set. Averaging all the 100 solutions for Test 5 gave the phases with a map correlation coefficient 0.95 with respect to the exact binary phases.

 

6.4. The use of observed magnitudes

 

            When working with real objects, binary magnitudes are not known and must be estimated somehow. In the following test, the set of observed magnitudes was used to estimate the binary ones. The grid 8*8*8 was chosen for this test as it allows one to solve BIP problems in a reasonable time using the existing software. On the other hand, the approximation of the binary structure factors magnitudes using the observed ones is poor at this grid size. This may significantly influence the results. In order to get more reliable results, BIP methods applicable to larger grids are necessary. The gap in the inequalities (6.5) was reduced to 25% of the estimated  value for acentric structure factors, and to 20% for the centric ones. After 100 runs of WSATOIP with random initial assignments, the obtained solutions were aligned and averaged. The found average solution revealed essential features of the 12Å resolution synthesis and had the map correlation coefficient (Lunin & Woolfson, 1993) equal to 0.74 with respect to the exact phases. Fragments of the obtained synthesis overlapped with the atomic model for Protein G are shown in Fig.2.

 

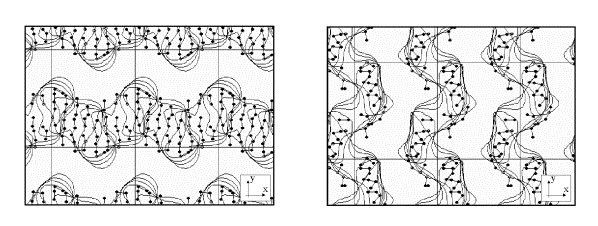
Fig.2. Fragments of BIP-phased Fourier synthesis superimposed with C_a atoms of the model for Protein G: a) projection of the slice z=-2 : 2/40 containing b-sheets; b) projection of the slice z=6:14/40 containing a-helices. The shown contour isolates 35% of the unit cell volume (0.4s cut-off level).

7. Conclusions

 

            The theoretical part of this work shows how the crystallographic phase problem can be reduced to the solution of a system of linear inequalities in binary variables. The practical tests with simulated and experimental protein data illustrate the high potential of this new approach. Crystallographic images found from such phasing can be used for further phase improvement or as an important complementary tool for other techniques like molecular replacement. In order to get images of a higher quality, further work on integer programming methods and their application in crystallography is in currently in progress.

 

Acknowledgements

 

            The work was supported by RFBR grants 00-04-48175 and 01-07-90317 and by the CPER Lorraine 2000-06. Programs O (Jones et al., 1991) and CAN (Vernoslova & Lunin, 1993) were used to prepare map illustrations. The authors thank L. Torlay for the computing assistance.

 

References

 

Bockmayr, A. & Kasper, T. (1998). INFORMS J. Computing 10, 287-300.

Derrick, J.P. & Wigley, D.B. (1994). J.Mol.Biol. 243, 906-918.

Johnson, E. L., Nemhauser, G. L. & Savelsbergh, M. W. P. (2000). INFORMS J. Computing 12, 2-23.

Jones, T.A., Zou, J.Y., Cowan, S.W. & Kjeldgaard, M. (1991). Acta Cryst. A47, 110-119.

Lunin, V.Y. & Woolfson, M.M. (1993). Acta Cryst. D49, 530-533.

Lunin, V.Y. & Lunina, N.L. (1996). Acta Cryst. A52, 365-368.

Lunin V.Y., Lunina N.L., Petrova T.E., Skovoroda T.P., Urzhumtsev A.G. & Podjarny A.D. (2000). Acta Cryst. D56, 1223-1232.

Sayre, D. (1951) Acta Cryst., 4, 362-367

Ten Eyck, L.F. (1973). Acta Cryst. A29, 183-191.

Vernoslova, E. A. & Lunin, V. Y. (1993). J. Appl. Cryst. 26, 291-294.

Walser, J.P. (1997). In Proceedings of the Fourteenth National Conference on Artificial Intelligence and Ninth Innovative Applications of Artificial Intelligence Conference, AAAI 97, IAAI 97, July 27-31, 1997, Providence, Rhode Island. AAAI Press / The MIT Press, 269-274

Walser, J.P. (1998). In Proceedings of the Fifteenth National Conference on Artificial Intelligence and Tenth Innovative Applications of Artificial Intelligence Conference, AAAI 98, IAAI 98, July 26-30, 1998, Madison, Wisconsin, USA. AAAI Press / The MIT Press, 373-379.