 |
|
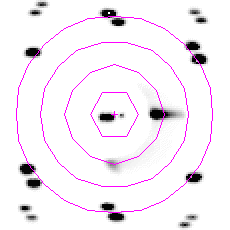
| A composite malto-porin diffraction pattern, between 100 and 400 Å resolution. | Human ceruloplasmin diffraction in the range 200 to 50Å resolution. |
It has long been the aim of crystallographers to be able
to determine phases from first principles. This is now routine in small
molecule crystallography, where the sample is usually long-lived in the
X-ray beam, and can give measurable diffraction to a resolution better than
1.2Å. Indeed, the size of molecule that can be tackled with these
Direct Methods is growing. When the 'Shake and Bake' approach was added
to the armoury, the size limit for structure determination went up to
around 600 atoms. But the resolution limitation holds fast, and although
many interesting proteins are within the target size limits, their
diffraction limit is still too poor for these methods.
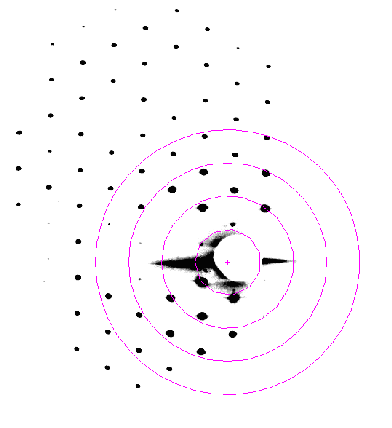
Low-resolution reflections are very important in
determining the molecular envelope, or the shape, of a protein. They can
be used to supplement phase information from elsewhere (e.g. from SIR or
single wavelength anomalous scattering). They can also provide a check for
models of the solvent contribution in structure refinement. Many groups,
including Gerard Bricogne's at Cambridge and the groups of Urzhumtsev and
Lunin (Puschino and Strasbourg), are interested in pursuing these approaches
to supplement phasing studies with SIR or single wavelength studies. Contact
addresses, literature references and further information for potential
users may be accessed at URL:
http://www.dl.ac.uk/SRS/PX/lowres/lowres.html
Technical Issues
Low-resolution terms, down to 250Å, are now easily accessible using the EMBL camera installed on station 7.2 at the SRS. Station 9.5 may also be used for this purpose. Low order reflections can of course be collected using a laboratory-based source, provided care is taken to collimate the beam, reduce the scatter and align a small beamstop. However, Station 7.2 has many features, which make it easy to access these data points:
The SRS keeps the flux sufficiently high after narrow
collimation (slits may need to be reduced to around 100 micron), so that
experiment turnround would be reasonable.
The standard wavelength of 1.488Å on Station
7.2 gives some advantage over the popular 0.9Å elsewhere, due to the
higher angle of diffraction, away from the primary beam. Longer wavelengths
are also accessible, to expand the reciprocal lattice further.
The Hamburg PX camera, which features a long
collimator, allows fine beam trimming for reduced divergence. It also has
a long beamstop translation track, so that the beamstop could be moved
a significant distance away from the sample, making the obscured angle
smaller.
The tuneability of Station 9.5 gives the added flexibility of repeating
the low-resolution data collection on either of an absorption edge of
one of the buffer components. Such data can be used for mask contrast
measurements, and therefore 'experimental measurement' of the phases.
 |

|
| A composite malto-porin diffraction pattern, between 100 and 400 Å resolution. | Human ceruloplasmin diffraction in the range 200 to 50Å resolution. |
Over the last decade, a variety of approaches have been
used to solve the phase problem directly, at low resolution. None of them
have come into common usage, perhaps because they are still in need of
development, but also perhaps due to the pressure on synchrotron facilities
for a higher throughput, therefore ignoring the 'less important'
low-resolution terms. Some of the methods are briefly outlined here:
1) The Few Atoms Method (FAM):
Lunin, Urzhumtsev et al.1,2,3,4 have used a
small number of large spheres to approximate the solvent part of the protein.
These 'atoms' would be refined against 8Å data, in a fashion similar
to real atoms, after substituting scattering factors of a sphere for the
atomic scattering factors. This approach worked reasonably well for mask
determination, but could not provide any extra phasing information up to
3Å, where atoms become interpretable. Non-crystallographic symmetry
might be able to break this deadlock, but it is not universally available.
The low resolution might also be too much of a challenge for the maximum
likelihood methods of phase extension.
2) The Sphere of Atoms Approach (SA):
Harris8 used a sphere of point scatterers
(water molecules), placed at uniform intervals within the sphere surface,
to maintain the atomicity of the simulation. The whole sphere would then
be 'refined' by systematic translations along the 3 axes, while checking
to exclude symmetry clashes, in a translation function analogy. Although
this approach worked for some test cases, it was computationally expensive
(back in 1994, using a micro-Vax). It also had very poor discrimination
towards the shape of the solvent region, which may be a cylinder or a
dumbbell or any other complex shape. There was only one shape, that of
a sphere, that was applied. This method too required the very low-resolution
terms, and had the same limitation as above regarding phase extension to
around 3.0Å.
3) Random Placement of Waters (RPW):
Subbiah5,6,7 used a random distribution of
water molecules as a starting point. He then moved each one in turn, by a
random distance, in a random direction and then decided whether the move
was 'Good' or 'Bad' according to a number of conditions. The total number
of water molecules used was usually around 2/3 of the C-alpha atoms in
the protein. This method appeared to work well, but there was an equal
likelihood of the water molecules converging into solvent or protein mask.
Methods were developed to distinguish between one and the other, and they
seem to work well. Although this method could work with routine PX data
sets, i.e. those lacking the low-resolution terms, its performance was
enhanced by their presence.
4) Genetic Algorithms (GA):
This approach starts by defining spherical volume
elements covering an arbitrary unit-cell, useful for solution scattering
simulations (Chacón et al.9). See also URL
http://srs.dl.ac.uk/fcis/fcis/dalai_ga . Then, each sphere is randomly
assigned as occupied or unoccupied, by setting a bit in the binary string.
A few permutations of the string are tested against the data for hierarchical
ranking. 'Daughter' strings may be generated, by combining equally ranked
strings. Other string manipulation tactics may be employed, e.g. dividing
a string in half and then combining it with another half string. An elegant
feature of this approach would emerge, if various starting combinations
were farmed out to a computer network, to share out the load. The need to
duplicate the data points would necessitate a smallish data set, well
suited to the low-resolution exercise. Other work with this approach is
also underway within the Bricogne team.
The Way Forward
The different approaches are sufficiently disparate in philosophy, but they are more further apart pragmatically. FAM is allied with the CCP4 package, SA is heavily dependent on it, although no optimised program was ever written. RPW evolved independently of CCP4, and further evolution is still possible. The 'Pantos' implementation of GA also evolved independently of CCP4, and could be easy to port, although that may have been done already in Cambridge.
More importantly, the principles behind these approaches have to be extended. As a first step it would be straightforward to envisage an amalgamation of the different methods into one program, brought up to date to exploit the current computer technology. Each method would be applied at a particular stage, and after an initial period of gathering experience, the optimum order would be quickly established.
Another scenario might follow this path: FAM/GA
produced crude masks provide a starting envelope, which would be
filled with matched spheres of point scatterers for SA applications.
Then the spheres would be made smaller and their number increased to
keep filling the surviving mask. This in turn would provide a starting
set of waters for RPW runs, with an increasing number of waters until
a reasonable fraction of the protein had been placed. Because FAM
selects the protein region, there is no risk that the subsequent SA
and RWP runs would coalesce to the wrong region. At this stage, a
round of ARP refinement might complete the phasing to the highest
resolution of the data set. The resultant map then would be ready
for all the manipulation techniques of DM, for instance, and an easy
interpretation should become feasible.