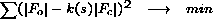Newsletter contents...

The Effect of Overall Anisotropic Scaling in Macromolecular Refinement
Garib N. Murshudov1,2*,Gideon J. Davies1, Mikhael Isupov3, Szymon Krzywda4, Eleanor J. Dodson1.
- 1Chemistry Department, University of York, York, U.K.
- 2CLRC, Daresbury Laboratory, Warrington, Daresbury, U.K.
- 3Chemistry Department, University of Exeter, Exeter, U.K.
- 4Crystallography Department, Faculty of Chemistry, Adam Mickiewicz University, Poznan, Poland,
- *e-mail garib@yorvic.york.ac.uk
1. Introduction
Parametrisation is still one of major problems of refinement
programs. This includes parameters of individual atoms, molecules and the whole
crystal structure. All parametrisations depend on available experimental data
and the current stage of structural analysis. In this note we discuss the
importance of overall anisotropic scaling during refinement and give several
examples where it has improved refinement substantially.
It was noted by S.Gamblin (1996): ``in the absence of an overwhelming
argument(such as cubic space group), it is always safest to assume that
diffraction is anisotropic''. This fact should be taken into account
in refinement as well as in data collection strategy and data processing.
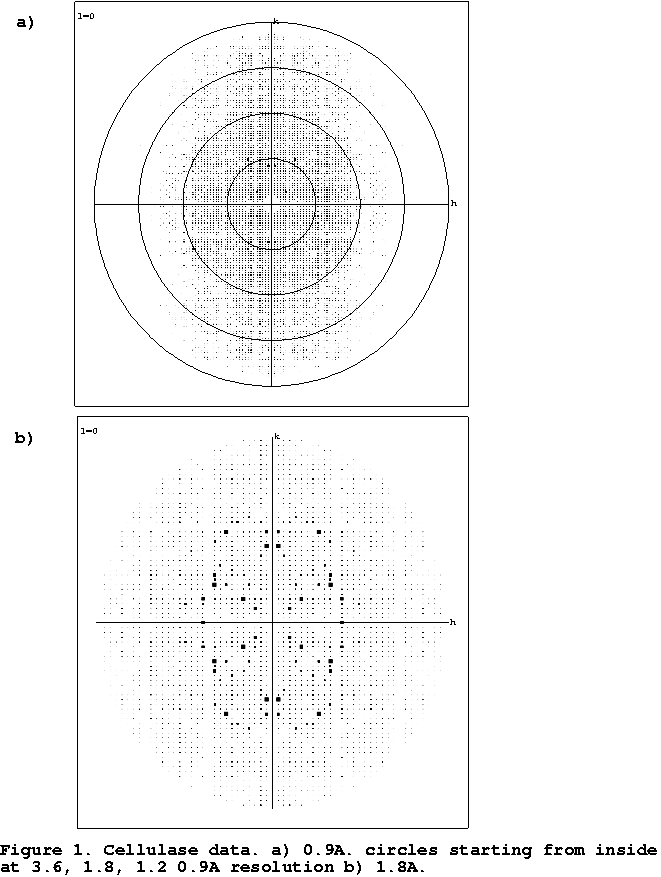
Figure
1 shows that sometimes only at high resolution does the anisotropicity of data
becomes apparent on the diffraction images. Anisotropicity of data might also
cause problems in data collection. If one accidentally collects
the first image in the direction of high thermal motion, one might not make the optimal decision for data
collection. An image perpendicular to the first should also be collected to
observe the true behaviour of the crystal.
The anisotropicity of the data should be taken into account during the data processing stage. This is possible with the CCP4 SCALA program, written by Phil Evans. In the absence of prior information about the contents of the crystal, refinement
of the overall anisotropicity at the data processing stage will remain
ill determined. In that case, any residual anisotropy should be
taken into account at the refinement stage or alternatively refinement and data
processing could be alternated. An even better
approach would be simultaneous refinement and data processing, but this would only be possible if the structure had already been solved.
In the first ever paper on least-squares refinement of crystal structures,
Hughes (1941) noted the existence of anisotropicity and described improved refinement behaviour by the introduction of anisotropic scale factors. It is
surprising that in highly mobile and large structures, such as proteins, this fact has not been taken into account until recently.
2. Sources of anisotropicity
Several factors contribute to apparent atomic anisotropicity. The crystal
itself (except in a cubic space group) is, in general, an anisotropic field, so
it is to be expected that the data collected from it may exhibit overall
anisotropicity. Freezing and/or addition of substrates will usually change the
anisotropicity of the crystal, in general increasing it.
A second source of anisotropicity is the movement of whole molecules as a rigid
bodies within the crystal lattice. This can be described by TLS parameters
(20 more per molecule) which are independent of the crystal form (Schomaker and
Trueblood 1968). The RESTRAIN program (Moss et al., 1996) is able to evaluate these, and the
correction has been shown to be valuable in some situations.
A third source of anisotropicity is vibration along torsion angles. In
principle this might be described by refining the torsion angles themselves,
and estimating their displacement parameters. However there are problems, since
these parameters are highly correlated and such refinement may be sensitive
to small perturbations of one or several of these. It may be better to deduce
the displacement parameters of the torsion angles from the individual
anisotropic atomic U values.
To summarise, the observed atomic anisotropic U values can be written as:
|
Uatom;overall = Ucrystal + UTLS + Utorsion + Uatom |
| (1) |
where Uatom;overall is the overall anisotropic U value,
Ucrystal is the contribution of crystal anisotropicity, UTLS
that of
model anisotropicity (TLS), Utorsion that of motion about torsion angle
and finally Uatom that of the atomic anisotropicity along and across
covalent bonds. Cruickshank (1956) noted that removing the Ucrystal made
the refinement of individual anisotropic U values more stable, and it seems
reasonable to apply these simple corrections to remove the modes related to
Ucrystal and UTLS.
Care should be taken in the refinement of these different contributions as they are highly correlated. To
overcome this difficulty they could be refined at the different levels. I.e. first
Ucrystal, second UTLS, third Utorsion and finally
Uatom, or alternatively refine Ucrystal, UTLS and along internal degrees of freedom as described by Diamond (1990).
Ucrystal is in principle sum of two
factors: 1) those remaining after data processing and 2) common mode from UTLS.
Here effect of the anisotropic scaling only will be discussed. For refinement
of individual atomic anisotropic thermal parameters see Murshudov et al. (1998)
3. Anisotropic Scaling
For anisotropic scaling, at each cycle of refinement the least-squares residual is
used to derive overall parameters:
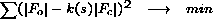 | (2) |
where the scale factor k = k0 e-hT U* h. U* is symmetric reciprocal
space anisotropic tensor. The space group puts constraints on the anisotropic
U tensor. For example, cubic space groups do not have an overall anisotropic U.
The space group P42 21 2 has 2 parameters and so on. In the implementation in the program REFMAC (Murshudov et al. 1997) this fact has been taken into account. As in this treatment anisotropic U is the difference between the observed and
calculated structure factors, there is no need to use positive definite
constraints. At each cycle of refinement, the program refines anisotropic
scale factors and applies them to calculated ones. There is also an option to apply
anisotropic scale to the observed structure factors. At this stage,
application of this option is not recommended since it changes the observed structure
factors. Thus, the calculated R-values would not be comparable with each other. If
anisotropic U values would be applied to observed structure factors then:
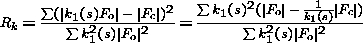 | (3) |
It is clear from this equation that at each cycle calculated R-value is in fact
weighted R-value with weights k12(s), where k1(s) = [1/ k(s)]. If k(s) is refined at each cycle then behaviour of R and Rk could be different.
4. Examples of application
All the examples given here are structures which have previously been refined
with isotropic scale factors. When
refinement of anisotropic scale factors became available they were applied to
different test cases. In all cases application of anisotropic scale factors
not only improved R and R-free but also refinement that had apparently
converged restarted. It is important to note, that in addition to R values, the
geometric parameters of the model improved significantly and difference maps
became cleaner.
- Native Catalase at 1.5Å
- Crystals of catalase from the
bacterium Mycrococcus lysodeikticus are almost perfect. Data from these
crystals have now been collected at 0.9Å resolution. Even in this case one
can see that anisotropic scale factor improves R-value and free R-value
(Table 1)
- Catalase frozen at 1.96Å
- Data from catalase soaked in peracetic acid
solution were used in order to obtain the reaction intermediate. Data were collected, from a frozen crystal, using
CuKa radiation and the RAXIS II as detector. In this case it can
be seen that effect of anisotropic scaling is much larger than in native room
temperature data (Table 1).
- Cellulase
- Data for this enzyme were collected from frozen crystals in
the home laboratory to 1.6Å resolution and the MIR structure determination
was essentially trivial (Davies et al., 1998) The refinement, although
straightforward, converged with unusually high values for both R and Rfree,
both above 20%. It was only upon collection of atomic (0.9Å) resolution data
that the anisotropic nature of the diffraction became easily apparent to the
authors from inspection of the diffraction images. At this point, the
anisotropic data scaling became available resulting in immediate reductions
in R and R free of over 6% (Table 1).
- Myoglobin
- This case was one of the prime reasons for speeding up the
implementation of
anisotropic scale factor refinement. There were 10 different data sets of
mutant and native myoglobins with different complexes. All data sets were
collected from frozen crystals. Refinement with overall isotropic B values
stuck with R 22%, R-free around 29%. Refinement of overall anisotropic scale
factor immediately reduced R-value and free R-value (Table 1).
- Oxoindolyl-L-alanyn complexed tryptophanase
- The complex of tryptophanase from
P.vulgaris with competetitve
inhibitor Oxindolyl-L-alanine have been crystallised in the space group
P21212 with a=152.480 , b= 213.694 , c=63.518 which was different from
holotryptophanase crystals. The structure has been solved by molecular
replacement using
the holotryptophanase coordinates. The conventional REFMAC refinement at
18-3 Å converged with R/R-free = 28.4/31.3%. Refinement with
anisotropic scaling reduced R/R-free to 24.88/27.8. Moreover, the
refinement went on to R/R-free=18.0/24.7 (Table 1)
5. Conclusions
Examples given here show that application of anisotropic scale factors improves the refinement. The current implementation is only a partial solution to the problem
of anisotropicity and the general problem of scaling observed and calculated
structure factors. A better solution would be to use likelihood functions which contain
information about scale factors, model errors and partiality, the
experimental uncertainty of observed structure factors, NCS, phase information
and any other available information.
Another problem related to anisotropic scaling is the overall molecular motion
(TLS) in the unit cell. Future development of REFMAC will incorporate this information. This can be achieved easily since the fast refinement of individual U values by FFT now is available.
In principle, the treatment of anisotropic U values should start from the data
processing so that many factors contributing to anisotropic scale factor could be accounted for. Then the refinement protocol could be used to model the residual
overall anisotropic scale factor.
Acknowledgements
We thank the members of the Structural Biology Laboratory,Department of
Chemistry, University of York for testing the program.
GNM is supported by BBSRC postdoctoral fellowship awarded to CCP4 (grant
B05273), GJD by the Royal Society, EJD by the MRC, MI by the BBSRC.
References
- CCP4. Collaborative Crystallographic Project, Number
4. (1994) Acta Cryst. D50, 760-763
- Cruickshank, D.W. (1956) Acta Cryst. 9, 747-753
- Davies, G.J., Dauter, M., Brzozowski, A.M., Bjornvad, M.E., Andersen, K.V. &
Schulein, M. (1998) Biochemistry 37, 1926-1932
- Diamond, R. (1990) Acta Cryst. A46 425-435
- Gamblin, S.J. (1996) in Macromolecular Refinement. Proceedings of the CCP4 Study Weekend Ed. Dodson,E., Moore,M., Ralph,A., Bailey, S. 163-170
- Hughes, E.W. (1941) J. Am. Chem. Soc. 63, 1737-1752
- Isupov et al., manuscript in preparation
- Murshudov, G.N., Lebedev, A., Vagin, A.A., Wilson, K.S., Dodson, E.J. (1998) submitted to Acta Cryst. D
- Murshudov, G.N, Melik-Adamyan, W.R., Grebenko, A.I., Barynin, V.V., Vagin, A.A., Vainshtein, B.K., Dauter, Z. & Wilson, K.S. (1992) FEBS letters 312, 127-131
- Murshudov, G.N., Vagin, A.A. & Dodson, E.J. (1997) Acta Cryst.
D53, 240-253
- Moss, D.S., Tickle, I.J., Theis, O. & Wostrack, A. in ``Macromolecular refinement'' Proceedings of the CCP4 Study Weekend, 105-113, Ed. Dodson, E., Moore, M., Ralph, A. & Bailey, S. CCLRC, Dareesbury Laboratory
- Schomaker, V. & Trueblood, K.N. (1968) Acta Cryst. B24 63-76
Table 1: Effect of anisotropic scaling
|
|
| MLC1 | MLC2 | CELL | MB | OIA
|
| d(Å) | 1.5 | 1.96 | 1.8 | 1.8 | 1.5
|
| R/R-free(iso %) | 11.7/14.0 | 17.3/22.6 | 20.2/25.1 | 22.1/28.8 | 28.4/31.3
|
| R/R-free(aniso %) | 11.6/13.9 | 15.1/20.6 | 14.3/18.0 | 20.6/27.0 | 18.0/24.7
|
| B11 | -0.3 | -3.4 | 9.1 | 5.6 | -9.8
|
| B22 | -0.3 | -3.4 | -4.2 | 1.0 | -15.5
|
| B33 | 0.7 | 7.1 | -4.8 | -6.2 | 33.6
|
| B12 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0
|
| B13 | 0.0 | 0.0 | 0.0 | 2.9 | 0.0
|
| B23 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
MLC1 - MLC native data collected at room temperature
MLC2 - MLC soaked in peracetic acid collected from frozen crystals
MB - Myoglobin collected from frozen crystals
OIA - Oxiindolyl-L-alanine complex of Tryptophanase
CELL - Cellulase
B11, B22, B33, B12, B13, B23 are elements of anisotropic B tensor. B = 8p2U
Figure 1:
 | (2) |
Newsletter contents ...