Multiwavelength Anomalous Diffraction in Macromolecular
Crystallography
Janet L. Smith
Department of Biological Sciences
Purdue University
West Lafayette, Indiana 47907 USA
Introduction
Multiwavelength anomalous diffraction (MAD) is the fastest growing method of
structure determination in macromolecular crystallography. At least
twenty-five new structures solved with MAD were published in the past year.
Many factors contribute to the growth of MAD, and its future is extremely
bright. The experience gained over the past several years is now being
generalized to make MAD more accessible. This paper aims to present a
practical overview of MAD. I first review the observational equation for MAD
and describe the basis of the phasing signal and how it is estimated for
specific problems. This is followed by a discussion of the design of a MAD
experiment, schemes for data analysis and phasing, and considerations in
solving the anomalous-scatterer partial structure. Finally, there is a
discussion of selenomethionine as a phasing vehicle. More comprehensive
reviews of MAD have been published by W. A. Hendrickson, who pioneered its
development and application in macromolecular crystallography (Hendrickson,
1991; Hendrickson & Ogata, 1997).
Theoretical Basis
Electrons bound in atomic orbitals have specific resonant frequencies
corresponding to allowed transitions. Anomalous scattering is the
manifestation in X-ray diffraction of these resonance effects. The resonant
frequencies of most chemical elements in biological macromolecules are far
below the energies used for diffraction experiments, and their anomalous
scattering is thus negligible. However, elements of atomic number
24 through 92 have resonant frequencies between 6 keV ( =
2Å) and 40 keV (
=
2Å) and 40 keV ( = 0.3Å), which give rise to detectable
effects in X-ray scattering from macromolecular specimens labeled with these
elements. Information about the phase of the scattered X-rays can be derived
from the resonance effects, or anomalous scattering. Anomalous scattering is
an atomic property and thus enters the equations for X-ray diffraction in the
expression for the atomic scattering factor (f), which is the sum of "normal"
atomic scattering factor f0 and a complex "anomalous" correction having real
(f') and imaginary (f") components:
= 0.3Å), which give rise to detectable
effects in X-ray scattering from macromolecular specimens labeled with these
elements. Information about the phase of the scattered X-rays can be derived
from the resonance effects, or anomalous scattering. Anomalous scattering is
an atomic property and thus enters the equations for X-ray diffraction in the
expression for the atomic scattering factor (f), which is the sum of "normal"
atomic scattering factor f0 and a complex "anomalous" correction having real
(f') and imaginary (f") components:
f = f0 + f' + if".
The breakdown of Friedel's law caused by the imaginary component of anomalous
scattering (f") has been used for many years as a source of phase information
in macromolecular crystallography. Wavelength-tunable synchrotron radiation
allows the real component (f') to be used as well, providing the opportunity
for direct phasing through combination of the orthogonal effects of f' and f".
MAD exploits differences in the observed diffraction intensities caused by
differential f' and f" values at different X-ray wavelengths to achieve such
direct phasing.
The formulation of the MAD observational equation used here is based on that
of Karle (1980) as modified by Hendrickson et al. (1985).
| Fobs+/-|2 = |FT|2 + a
Fobs+/-|2 = |FT|2 + a  |FA|2
+ b
|FA|2
+ b  |FT||FA|cos(
|FT||FA|cos( T-
T- A)
+/- c
A)
+/- c  |FT||FA|sin(
|FT||FA|sin( T-
T- A), [1]
where a
A), [1]
where a  = (f"
= (f" 2+f'
2+f' 2)/(f0)2,
b
2)/(f0)2,
b  = 2f'
= 2f' /f0
and c
/f0
and c  = 2f"
= 2f" /f0.
/f0.
This formulation is distinguished from many others relating phases to anomalous
scattering by Karle's insight that the real (| FA'|)
and
imaginary (|
FA'|)
and
imaginary (| FA"|) structure amplitudes, due to f' and
f",
respectively, can be expressed as products of scattering factor ratios and
normal structure amplitudes, due to f0:
FA"|) structure amplitudes, due to f' and
f",
respectively, can be expressed as products of scattering factor ratios and
normal structure amplitudes, due to f0:
| FA'| = (f'
FA'| = (f' /f0)|FA|
and |
/f0)|FA|
and | FA"| = (f"
FA"| = (f" /f0)|FA|.
/f0)|FA|.
Wavelength-dependence and structure-dependence are thus separated into
different quantities. All wavelength dependence is in the anomalous scattering
factors, f' and
f"
and
f" , which do not depend on atomic
positions, and all structure dependence is in the normal structure factors
FT and FA, which do not depend on wavelength. The structure
factor FT represents normal scattering from the total structure, and
FA represents normal scattering from the partial structure of anomalous
scatterers. An Argand diagram showing the relationships of these structure
factors has been published (Smith, 1991). Eq. 1 describes the case for one
type of anomalous scatterer. In general, Eq. 1 will relate experimental
observations to unknown quantities whose number equals twice the number of
anomalous-scatterer types plus one, here |FT|, |FA| and
(
, which do not depend on atomic
positions, and all structure dependence is in the normal structure factors
FT and FA, which do not depend on wavelength. The structure
factor FT represents normal scattering from the total structure, and
FA represents normal scattering from the partial structure of anomalous
scatterers. An Argand diagram showing the relationships of these structure
factors has been published (Smith, 1991). Eq. 1 describes the case for one
type of anomalous scatterer. In general, Eq. 1 will relate experimental
observations to unknown quantities whose number equals twice the number of
anomalous-scatterer types plus one, here |FT|, |FA| and
( T-
T- A
) for one anomalous-scatterer type.
A
) for one anomalous-scatterer type.
The MAD observational equation (Eq. 1) involves no approximations, and the
accuracy of MAD phases is limited only by the precision of the diffraction
data. This is in contrast to isomorphous replacement where phase accuracy is
limited most severely by breakdown of the assumption of isomorphism of native
and derivative crystals. The new prominence of MAD is due primarily to a
significant improvement in the quality of diffraction data in general. This
comes from the ability to measure better data faster thanks to widespread
adoption of cryocooling techniques and to improvements in synchrotron sources
and X-ray detectors.
Anomalous scattering factors
Anomalous scattering factors in the region of an absorption edge are sensitive
to the chemical environment of the absorbing atom, and are significantly
enhanced by sharp spectral features in many cases. Therefore, f" and f' for
anomalous scatterers in macromolecules cannot be calculated as free-atom
anomalous scattering factors (Cromer & Liberman, 1970a,1970b), which are
accurate estimates for all chemistries at energies away from absorption edges.
Several laboratories have schemes for extracting anomalous scattering factors
f' and f" from X-ray spectra, none of which has been published in rigorous
detail. However, all exploit the fact that the imaginary component of
anomalous scattering f" is proportional to the atomic absorption coefficient
ua, which can be obtained easily from raw X-ray fluorescence or transmission
data. The scheme of Hendrickson et al. (1988) is described briefly
here and illustrated in Fig. 1. The X-ray spectrum of the labeled
macromolecule, typically a macromolecule single crystal, is measured as
fluorescence through the edge of interest (Fig. 1a). Regions of the
experimental spectrum slightly away from the edge are fit to theoretical values
using the program XASFIT in order to place the experimental spectrum on an
absolute scale (Fig. 1b). Theoretical values are obtained from a program by
Don Cromer, modified by Wayne Hendrickson to produce spectra rather than f' and
f" at single energies and variously called FPRIME, SPECTRUM or CROMER. Care
must be taken to measure enough edge-remote points for reliable fit of the
experimental spectrum, which may be quite noisy. A narrow region around the
absorption edge is then cut from the scaled experimental spectrum and spliced
into the theoretical spectrum. From the hybrid spectrum of f" values thus
obtained, f' values are calculated by Kramers-Kronig transformation:
 [2]
[2]
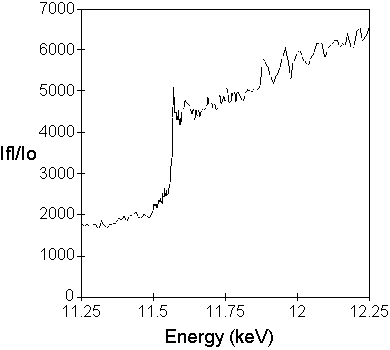

Figure 1
A. Fluorescence spectrum (I/I0 on an arbitrary scale) through the Pt LIII
absorption edge from a single crystal of 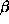 -hydroxydecanoyl thiolester
dehydrase (Leesong et al., 1996). A single methionine amino acid of the
crystalline protein was labeled with Pt by soaking in a solution of K2PtCl4.
-hydroxydecanoyl thiolester
dehydrase (Leesong et al., 1996). A single methionine amino acid of the
crystalline protein was labeled with Pt by soaking in a solution of K2PtCl4.
B. Scaling of fluorescence data to theoretical atomic absorption coefficients
(ua). The raw fluorescence spectrum was fit to the theoretical spectrum for
the Pt LIII edge using the program XASFIT. The scaled experimental spectrum is
shown superimposed on the theoretical free-atom spectrum.
 C. Hybrid f" and f' spectra for the Pt LIII edge. Using the program KRAMIG,
the edge region has been cut from the experimental spectrum in B and spliced
into the theoretical spectrum, ua converted to f", and f' calculated from f" by
Kramers-Kronig transformation (Eq. 2).
C. Hybrid f" and f' spectra for the Pt LIII edge. Using the program KRAMIG,
the edge region has been cut from the experimental spectrum in B and spliced
into the theoretical spectrum, ua converted to f", and f' calculated from f" by
Kramers-Kronig transformation (Eq. 2).
where E is energy in eV and d is the energy increment of the f" spectrum being
transformed. In practice, the point of singularity for each f' (Ei = E) is not
included in the summation, and a transformation range of ~500 eV beyond the f'
being computed is sufficient to eliminate truncation effects. Splicing and f'
calculation (Fig. 1c) are done with the program KRAMIG.
Typical anomalous scattering factors, f"max and f'min, estimated from X-ray
spectra of protein crystals taken at MAD experimental stations, are given in
Table 1 for several elements. In addition to the electronic environment of the
anomalous scatterer, the energy dispersion of the incident X-ray beam also
influences the values of anomalous scattering factors in the edge region.
Table 1. Typical anomalous scattering factors
Element f0 Edge  f'min
f'min  f"max Reference
(e-) (Å) (e-) (Å) (e-)
Fe 26 K 1.7402 -9 1.7380 5 Hendrickson et al.,1988
1.7425 -8 1.7390 4 Smith et al.,1994
Cu 29 K 1.3790 -8 1.3771 4 Guss et al., 1988
Zn 30 K 1.2826 -9 1.2818 4 Zhang et al., 1995
Se 34 K 0.9793 -11 0.9792 6 Wu et al., 1994
Br 35 K 0.9207 -7 0.9196 4 Ogata et al., 1989
Sm 62 LII 1.6959 -16 1.6952 17 Tomchick et al., 1996
Ho 67 LIII 1.5363 -28 1.5356 20 Weis et al., 1991
Yb 70 LIII 1.3857 -33 1.3853 35 Shapiro et al., 1995
W 74 LIII 1.2136 -24 1.2123 19 Egloff et al., 1995
Os 76 LIII 1.1402 -23 1.1397 20 Cate et al., 1996
Pt 78 LIII 1.0720 -21 1.0714 13 Fig. 1c
Hg 80 LIII 1.0094 -18 1.0057 10 Tesmer et al., 1994
1.0095 -25 1.0063 12 Krishna et al., 1994
U 92 LIII 0.7213 -21 0.7208 12 Glover et al., 1995
f"max Reference
(e-) (Å) (e-) (Å) (e-)
Fe 26 K 1.7402 -9 1.7380 5 Hendrickson et al.,1988
1.7425 -8 1.7390 4 Smith et al.,1994
Cu 29 K 1.3790 -8 1.3771 4 Guss et al., 1988
Zn 30 K 1.2826 -9 1.2818 4 Zhang et al., 1995
Se 34 K 0.9793 -11 0.9792 6 Wu et al., 1994
Br 35 K 0.9207 -7 0.9196 4 Ogata et al., 1989
Sm 62 LII 1.6959 -16 1.6952 17 Tomchick et al., 1996
Ho 67 LIII 1.5363 -28 1.5356 20 Weis et al., 1991
Yb 70 LIII 1.3857 -33 1.3853 35 Shapiro et al., 1995
W 74 LIII 1.2136 -24 1.2123 19 Egloff et al., 1995
Os 76 LIII 1.1402 -23 1.1397 20 Cate et al., 1996
Pt 78 LIII 1.0720 -21 1.0714 13 Fig. 1c
Hg 80 LIII 1.0094 -18 1.0057 10 Tesmer et al., 1994
1.0095 -25 1.0063 12 Krishna et al., 1994
U 92 LIII 0.7213 -21 0.7208 12 Glover et al., 1995
Energy
(keV) = 12.39854/ (Å)
(Å)
Estimation of the Magnitude of the MAD signal
Knowledge of anomalous scattering factors allows estimation of the MAD signal
for a specific anomalous scatterer in a specific macromolecule. The orthogonal
components of the phasing signal, due to the real and imaginary anomalous
scattering factors f' and f", are estimated separately because both are
required for phase determination. The maximum MAD Bijvoet signal is due to
Bijvoet differences at the energy of peak absorption, or f"max, and is
proportional to 2f"max of Table 1. The maximum MAD dispersive signal is due to
wavelength differences between structure amplitudes at the energy of the
inflection point of the edge (f'min) and at a remote energy(f'remote), and is
proportional to |f'min-f'remote|.
The magnitude of the MAD phasing signal is estimated as the ratio of expected
Bijvoet or dispersive difference to expected total scattering of the
macromolecule. This is
based on calculation of expected structure amplitudes <|F|>, where
<|F|> =
 and
<|F|> =
and
<|F|> =
 for N atoms of identical f (Crick & Magdoff, 1956). The diffraction ratios
of interest to MAD (Hendrickson, 1985) are, for the dispersive signal,
for N atoms of identical f (Crick & Magdoff, 1956). The diffraction ratios
of interest to MAD (Hendrickson, 1985) are, for the dispersive signal,
 [3]
[3]
for N anomalous-scatterer sites with  1 chosen at f'min and
1 chosen at f'min and
 2 chosen for |f'
2 chosen for |f' 1-f'
1-f' 2|max, and, for the Bijvoet
signal,
2|max, and, for the Bijvoet
signal,
 [4]
[4]
with  chosen at f"max. These diffraction ratios are analogous to the
usual calculation of isomorphous signal from experimental data in which
chosen at f"max. These diffraction ratios are analogous to the
usual calculation of isomorphous signal from experimental data in which
 [5]
[5]
where f0 is for the heavy atom. Values for f0, f'min and f"max are those
in
Table 1. The denominator of all diffraction ratios is the expected total
scattering of the macromolecule, which can be estimated for 2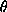 = 0 with
the expressions in Table 2.
= 0 with
the expressions in Table 2.
Table 2. Estimates of scattering strength for macromolecules,
<|FT|>
Macromolecule NA = # atoms NR = # residues MW = molecular weight
(e-) (e-) (e-)
Protein 6.70 (NA)1/2 (346 NR)1/2 (3.14 MW)1/2
DNA 7.20 (NA)1/2 (1128 NR)1/2 (3.87 MW)1/2
RNA 7.26 (NA)1/2 (1183 NR)1/2 (3.89 MW)1/2
A hypothetical example illustrates the issue of signal size in MAD vs.
isomorphous replacement. Consider a 500-residue protein and the MAD signal
generated by 10 Se anomalous scatterers. If f"max = 6 e-, f'min = -11 e-
and
f'remote = -4 e-, then by Eq. 4 the maximum Bijvoet signal will be ~6% of
|Fobs| and by Eq. 3 the maximum dispersive signal will be ~4% of
|Fobs|. By comparison, the isomorphous replacement signal generated by
one fully occupied Hg site (f0 = 80 e-) in the same protein will be ~14% of
|Fobs| by Eq. 5. For many typical examples the MAD signal is near the
noise level of moderate-quality diffraction data sets, whereas the isomorphous
replacement signal is easily detectable in data of moderate quality. On the
other hand, detection of the MAD signal is limited only by data quality whereas
lack of isomorphism will pollute the isomorphous replacement signal with
systematic error that cannot be removed. It is clear from the large number of
successful MAD experiments that a relatively weak phasing signal is by no means
an insurmountable problem.
MAD experimental design
Three important considerations distinguish the design and execution of a MAD
experiment from more familiar monochromatic experiments in macromolecular
crystallography. These are wavelength selection, data completeness and data
quality. A discussion of the design of beamline components for MAD
experiments is presented in another paper in this volume by A. W.
Thompson.
The largest MAD phasing signal is obtained at energies with the most extreme
values of f' and f", which correspond to the sharpest features of the
absorption edge. Therefore, it is critical to determine the position of the
absorption edge experimentally from the labeled macromolecule at the time of a
MAD experiment. Even when the position of the edge is well known, small
unanticipated chemical changes in the sample or energy changes in the X-ray
beam can reduce the MAD signal very significantly if the sharp edge features
are missed in selecting energies for data collection. Energies are selected at
the peak of sample absorption just above the edge ("Epeak" for f"max) to
optimize the Bijvoet signal and at the inflection point of the edge ("Edip" for
f'min) to optimize the orthogonal dispersive signal. The dispersive signal is
further optimized if a third energy remote from the edge ("Eremote") is chosen.
The choice of Eremote is experiment dependent, although it is typically above
rather than below the edge due to the larger Bijvoet signal. Eremote may also
be chosen to avoid complications from other edges or to obtain data at a
wavelength optimal for model refinement.
There has been much debate about the optimal number of data-collection
energies for successful phase determination by MAD. In the commonest MAD
experiment |F+| and |F-| are measured at each of Edip, Epeak
and
Eremote. If the difference in f' is large enough to produce a detectable
signal, then one could in principle obtain phases from three measurements:
|F+| and |F-| at Epeak and either |F+| or
|F-| at
Edip (Peterson et al., 1996). However, redundancy is one of the best
ways to minimize the effects of measurement error in macromolecular
crystallography. In the full three-energy experiment, the Bijvoet signal is
redundant because the remote energy is above the edge. The orthogonal
dispersive signal is redundant because two measurements are taken at each of
Edip and Eremote. There are several examples of even more redundant four- or
five-wavelength MAD experiments. While greater redundancy is desirable, it
should not be gained at the cost of good counting statistics. Unfortunately,
considerations of available beam time frequently preclude MAD experiments with
more than three energies.
The MAD phasing signal is derived from intensity differences that may be
similar in magnitude to measurement errors. Thus a general philosophy in the
design of a MAD experiment is to equalize systematic errors among the
measurements whose differences will contribute to each phase determination.
This is achieved for each single reflection by recording Bijvoet measurements
at all wavelengths from the same asymmetric unit of the same crystal at nearly
the same time. Bijvoet mates can be recorded simultaneously by alignment of
the crystal with a mirror plane perpendicular to the rotation axis, or Friedel
images can be recorded in an "inverse beam" experiment. (Friedel images are
related by 180o. rotation of the crystal about any axis perpendicular to the
incident beam, usually the data-collection axis). If crystal decay is a
problem, small blocks of Bijvoet data can be recorded at each of the selected
wavelengths before moving to another block of reciprocal space. When such a
data collection strategy is followed, the resulting MAD data set will
be complete with respect to recording all multiwavelength, Bijvoet
measurements for all regions of the reciprocal lattice that are covered in the
experiment. Coverage of reciprocal space can be monitored during the
experiment by a strategy program, if available, or by reduction of diffraction
images to integrated intensities for data from at least one wavelength.
Completeness of the MAD data set is at least as important as for any
diffraction experiment that will be used for phasing. If data, and hence phase
information, are incomplete, it may be difficult to reproduce the same beam and
sample conditions during a subsequent experiment, which is likely to occur only
after some weeks or months.
Measurement errors are of major importance in all areas of macromolecular
crystallography, but are the limiting factor in phase determination by MAD.
MAD data should be of high quality by the usual measures (Rsym, redundancy,
completeness), especially in experiments where the phasing signal is weak. In
the hypothetical 500-residue
protein with 10 Se anomalous scatterers, a 5% MAD signal will become
undetectable as it is exceeded by Rsym "noise". Thus data with good counting
statistics are of paramount importance. In a carefully designed experiment,
the effect of increasing Rsym with increasing 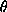 is mitigated somewhat
by equalizing systematic errors. Nevertheless, if Rsym (I) is 30% for the
outer shells of data, there will be virtually no detectable MAD phasing signal
for these reflections in the hypothetical example. Disappearance of the
phasing signal into Rsym noise is the major reason that useful MAD phases
generally are not obtained to the diffraction limit of crystals even though
anomalous scattering does not fall off with increasing
is mitigated somewhat
by equalizing systematic errors. Nevertheless, if Rsym (I) is 30% for the
outer shells of data, there will be virtually no detectable MAD phasing signal
for these reflections in the hypothetical example. Disappearance of the
phasing signal into Rsym noise is the major reason that useful MAD phases
generally are not obtained to the diffraction limit of crystals even though
anomalous scattering does not fall off with increasing 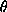 .
.
Data processing and scaling
Concerns about signal size dominate special schemes for handling MAD data.
Scaling strategies for MAD are discussed in detail elsewhere in this volume by
P. R. Evans. Special computer programs for scaling MAD data have been
developed (Hendrickson et al., 1988; Friedman et al., 1994). Two
general approaches to data handling for MAD have been employed.
The approach originally proposed by Hendrickson, known as "phase first, merge
later," represents the extreme interpretation of the scheme for equalizing
systematic errors - the individual observations constituting a multiwavelength
Bijvoet set, as determined by the data-collection strategy, are grouped
together and scaled as usual, but are merged with redundant measurements only
after phases are determined. Error estimates from the phasing or the agreement
of redundant phase determinations can be incorporated into weights for
averaging, or can be used to reject outliers. This approach involves
complicated, experiment-dependent bookkeeping to assemble exactly the correct
observations for each unmerged set.
A second approach, "merge first, phase later," is to scale and merge data at
each wavelength, keeping Bijvoet pairs separate, and then to scale data at all
wavelengths to one another. This is most easily and reliably done by scaling
all data against a common standard data set, which can be the unique data from
one wavelength with Bijvoet mates averaged. If the data collection followed
one of the strategies outlined above, then measurements for each unique
reflection are identically redundant, which itself minimizes systematic errors
in the amplitude differences used for phasing. The second approach is
computationally simpler than the first because it is experiment independent.
However, unanticipated, minor experimental disasters may be more difficult to
overcome in the "merge first, phase later" approach to data handling.
Approaches to MAD phasing
There are two general approaches to MAD phasing. One is to treat the problem
explicitly and solve the MAD observational equation (Eq. 1). This explicit
approach is embodied in the MADSYS package from the Hendrickson laboratory (Wu
& Hendrickson, 1996), in particular in the phasing program MADLSQ. The
other approach is to treat MAD phasing as a special case of multiple
isomorphous replacement (MIR). The pseudo-MIR approach is discussed elsewhere
in this volume by V. Biou and in two recent publications (Ramakrishnan &
Biou, 1997; Terwilliger, 1997). Both approaches have been quite successful,
and there are no hard-and-fast rules for which sorts of problems are more
amenable to which approach, rumors in the community notwithstanding. There are
advantages and disadvantages to both approaches.
The explicit approach provides the quantities |FT|, |FA| and
( T-
T- A). Estimates of the
anomalous scattering factors at the
wavelengths of data collection are required to fit the observations to the MAD
phase equation. These estimates can be refined within MADLSQ, so they need not
be highly accurate. A second calculation is required to obtain
A). Estimates of the
anomalous scattering factors at the
wavelengths of data collection are required to fit the observations to the MAD
phase equation. These estimates can be refined within MADLSQ, so they need not
be highly accurate. A second calculation is required to obtain  T from
the phase differences (
T from
the phase differences ( T-
T- A).
There are two advantages to the
explicit approach. First, it is amenable to the "phase first, merge later"
scheme of data handling because refinement of the anomalous-scatterer partial
structure is entirely separate from phase calculation. In this case
redundancies are merged to produce a unique data set at the level of the
derived quantities |FT|, |FA|, (
A).
There are two advantages to the
explicit approach. First, it is amenable to the "phase first, merge later"
scheme of data handling because refinement of the anomalous-scatterer partial
structure is entirely separate from phase calculation. In this case
redundancies are merged to produce a unique data set at the level of the
derived quantities |FT|, |FA|, ( T-
T- A) and their
error estimates. These error estimates or the agreement of redundant phase
determinations can be used to weight terms in a Fourier synthesis from
|FT| and
A) and their
error estimates. These error estimates or the agreement of redundant phase
determinations can be used to weight terms in a Fourier synthesis from
|FT| and  T. Phase probability coefficients (ABCDs) have
been
derived from the MAD phase equation (Pähler et al., 1990). The
second principle advantage of the explicit approach is calculation of an
experimentally derived estimate of the normal structure amplitude |FA|
for the anomalous scatterer. This is the quantity with which the partial
structure of anomalous scatterers is most directly solved and refined, and
therefore should be highly sought. However, while MADLSQ is quite successful
in the least-squares fit of the MAD phase equation to |Fobs| for
high-quality data, it is poorly conditioned to extracting |FA| from
noisy data and requires careful pruning of outliers from the |FA| values
produced. A Bayesian method of |FA| estimation (Terwilliger, 1994)
should be more robust than the least-squares procedure.
T. Phase probability coefficients (ABCDs) have
been
derived from the MAD phase equation (Pähler et al., 1990). The
second principle advantage of the explicit approach is calculation of an
experimentally derived estimate of the normal structure amplitude |FA|
for the anomalous scatterer. This is the quantity with which the partial
structure of anomalous scatterers is most directly solved and refined, and
therefore should be highly sought. However, while MADLSQ is quite successful
in the least-squares fit of the MAD phase equation to |Fobs| for
high-quality data, it is poorly conditioned to extracting |FA| from
noisy data and requires careful pruning of outliers from the |FA| values
produced. A Bayesian method of |FA| estimation (Terwilliger, 1994)
should be more robust than the least-squares procedure.
In the pseudo-MIR approach data at one wavelength are designated as "native"
data, which include anomalous scattering, and data at the other wavelengths as
"derivative" data. This approach has the advantage that nothing need be known
about the anomalous scattering factors prior to phasing. These quantities are
incorporated into heavy-atom atomic "occupancies" and refined along with other
parameters. Of course, the partial structure of anomalous scatterers must be
known, and refinement of the partial structure is concurrent with phasing. In
refinement of the "heavy atom" parameters, greater weight is given to the data
set selected as "native." This bias should be removed by the new
maximum-likelihood refinement of de La Fortelle and Bricogne (1997), which
treats data at all wavelengths as statistically equivalent. The amplitudes
|FA| are not determined in the pseudo-MIR approach, and the partial
structure is solved from Bijvoet differences between |F+| and
|F-| or dispersive differences between |F 1|
and
|F
1|
and
|F 2|, with wavelengths selected to optimize the signal. The
pseudo-MIR approach is used more frequently than the explicit approach due to
the greater familiarity of crystallographers with software for isomorphous
replacement.
2|, with wavelengths selected to optimize the signal. The
pseudo-MIR approach is used more frequently than the explicit approach due to
the greater familiarity of crystallographers with software for isomorphous
replacement.
Determination of the anomalous-scatterer partial structure
A prerequisite for MAD-phased electron density, regardless of the phasing
technique, is determination of the partial structure of anomalous scatterers.
As described above, the optimal quantities for solving and refining the partial
structure of anomalous scatterers are the normal scattering amplitudes
|FA|. Frequently |FA| values are not extracted from the MAD
measurements, and the largest Bijvoet or dispersive differences are used
instead. This involves the usual approximation of representing structure
amplitudes (|FA|) as the subset of larger differences
(||F+|-|F-|| or ||F 1|-|F
1|-|F 2||).
The approximation is accurate for only a small fraction of reflections because
there is no correlation between the phase of FP and the phase of
FA. However, it suffices for a suitably strong signal and a suitably
small number of sites. For virtually all structures determined by MAD, the
anomalous-scatterer sites have been located by Patterson methods. However,
the problem quickly becomes intractable by Patterson methods when there are
more than a handful of sites. This is a current challenge for MAD, where the
aim is to solve the macromolecule structure from one MAD data set using any
number of anomalous scatterer sites. Statistical direct methods clearly hold
the answer to this problem. Recent results are promising in this regard.
Bertrand et al. (1997) have solved a 12-atom Se partial structure in a
437-residue protein by direct methods using |FA|s, and S. Doublié
(personal communication) has solved a 15-atom Se partial structure in an
asymmetric unit of 108kDa using dispersive differences, also by direct
methods. These results open the door for routine MAD determination of quite
large structures with many anomalous scatterer sites. New direct methods
techniques, such as described in this volume in papers by G. M. Sheldrick, by
C. M. Weeks and by G. Bricogne, hold great promise for a major expansion in the
complexity of anomalous-scatterer partial structure that can be solved.
2||).
The approximation is accurate for only a small fraction of reflections because
there is no correlation between the phase of FP and the phase of
FA. However, it suffices for a suitably strong signal and a suitably
small number of sites. For virtually all structures determined by MAD, the
anomalous-scatterer sites have been located by Patterson methods. However,
the problem quickly becomes intractable by Patterson methods when there are
more than a handful of sites. This is a current challenge for MAD, where the
aim is to solve the macromolecule structure from one MAD data set using any
number of anomalous scatterer sites. Statistical direct methods clearly hold
the answer to this problem. Recent results are promising in this regard.
Bertrand et al. (1997) have solved a 12-atom Se partial structure in a
437-residue protein by direct methods using |FA|s, and S. Doublié
(personal communication) has solved a 15-atom Se partial structure in an
asymmetric unit of 108kDa using dispersive differences, also by direct
methods. These results open the door for routine MAD determination of quite
large structures with many anomalous scatterer sites. New direct methods
techniques, such as described in this volume in papers by G. M. Sheldrick, by
C. M. Weeks and by G. Bricogne, hold great promise for a major expansion in the
complexity of anomalous-scatterer partial structure that can be solved.
The correct enantiomorph for the anomalous-scatterer partial structure must be
determined ( A vs. -
A vs. - A)
in order to obtain an
electron-density image of the macromolecule. However, it cannot be determined
directly from MAD data. The correct hand is chosen by comparison of electron
density maps based on both enantiomorphs of the partial structure. Unlike the
situation for MIR, the density based on the incorrect hand of the
anomalous-scatterer partial structure is not the mirror image of that based on
the correct hand and contains no image of the macromolecule. The correct map
is distinguished by features such as a clear solvent boundary, positive
correlation of redundant densities, and a macromolecule-like density histogram.
If the anomalous scattering centers form a centric array, then the two
enantiomorphs are identical and both maps are correct.
A)
in order to obtain an
electron-density image of the macromolecule. However, it cannot be determined
directly from MAD data. The correct hand is chosen by comparison of electron
density maps based on both enantiomorphs of the partial structure. Unlike the
situation for MIR, the density based on the incorrect hand of the
anomalous-scatterer partial structure is not the mirror image of that based on
the correct hand and contains no image of the macromolecule. The correct map
is distinguished by features such as a clear solvent boundary, positive
correlation of redundant densities, and a macromolecule-like density histogram.
If the anomalous scattering centers form a centric array, then the two
enantiomorphs are identical and both maps are correct.
Selenomethionine
The most successful MAD phasing vehicle to date has been selenium in the form
of selenomethionine (SeMet). This particularly clever experiment was devised
by Wayne Hendrickson (1985), who also pioneered its use (Yang et al.,
1990; Hendrickson et al., 1990). Briefly, proteins are labeled with Se
by biological substitution of SeMet for methionine amino acids. This is
achieved by blocking methionine biosynthesis in the cells in which the protein
is produced and substitution of SeMet for Met in the growth medium. The
generality of the labeling scheme for proteins is the root of its success.
SeMet labeling technology is discussed in a recent review by Doublié
(1997).
SeMet incorporation has been done most frequently for proteins expressed in
E. coli strains that are auxotrophic for Met (strain DL41,
Hendrickson et al., 1990; strain B834, Leahy et al., 1994 and
Doherty et al., 1995; strain LE392, Ceska et al., 1996; strain
MIC88, Shamoo et al., 1995). Nearly complete incorporation has also
been reported in nonauxotrophic bacterial strains (E. coli strain BL21,
Harrison et al., 1994; E. coli strain XA90, Van Duyne et
al., 1994, Labahn et al., 1996), in a mammalian cell line (Lustbader
et al., 1995) and in baculovirus-infected insect cells (Chen & Bahl,
1991). Special precautions must be taken to prevent oxidation of SeMet
proteins. In almost all cases, somewhat higher-than-normal concentrations of
disulfide reducing agents, such as dithiothreitol or 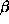 -mercaptoethanol,
are sufficient to protect SeMet from air oxidation to the selenoxide (Brot
et al., 1984). In a few cases, crystallization in an inert atmosphere
has been necessary (Dyda et al., 1994; Wu et al., 1994).
Because Se is a light element, the position of the K absorption edge moves to
slightly higher energy upon oxidation, and a mixture of oxidation states in a
sample crystal is predicted to obliterate the MAD signal.
-mercaptoethanol,
are sufficient to protect SeMet from air oxidation to the selenoxide (Brot
et al., 1984). In a few cases, crystallization in an inert atmosphere
has been necessary (Dyda et al., 1994; Wu et al., 1994).
Because Se is a light element, the position of the K absorption edge moves to
slightly higher energy upon oxidation, and a mixture of oxidation states in a
sample crystal is predicted to obliterate the MAD signal.
Methionine is a particularly attractive target for anomalous scatterer
labeling. The hydrophobic side chain of methionine, which carries the sulfur
atom to be substituted by selenium, is usually buried in the hydrophobic core
of globular proteins and is therefore relatively better ordered than are
surface side chains. Evidence for isostructuralism of Met and SeMet proteins
comes from the labeling experiment itself. All proteins in the biological
expression system have SeMet substituted for Met at levels approaching 100%.
The cells are viable, therefore the proteins are functional and isostructural
with their unlabelled counterparts to the extent required by function.
The natural abundance of methionine in soluble proteins is approximately one
in fifty amino acid residues. The N-terminal Met is not included in this
estimate because, if present, it is usually disordered. Using Eqs. 3 and
4, this provides a maximal MAD phasing signal of 4-6% of |F|, easily
detectable in strongly diffracting protein crystals and detectable with careful
data collection from crystals of moderate quality. To improve the phasing
signal, in a few cases Met has been substituted for other amino acids by
site-directed mutagenesis (Leahy et al., 1994, 1996; Skinner et
al., 1994; Tong et al., 1996).
SeMet labeling is now part of the repertoire of protein crystallography, and
has broader applicability than for MAD phasing alone. This comes from the
relative ease of incorporation of the SeMet label, from the remarkable
structural similarity of SeMet and wild type proteins, and from the uniformity
and completeness of labeling. Crystals of SeMet proteins are usually
isomorphous with those of the wild type, and consequently can be used as
isomorphous derivatives. The isomorphous signal comes from the excess of 18
electrons in Se relative to S, making the SeMet isomorphous phasing signal
(~10% of |F|, Eq. 5) about twice as strong as the SeMet MAD phasing
signal (4-6% of |F|). In most cases SeMet derivatives are more
isomorphous, and certainly more rationally produced, than are heavy-atom
derivatives produced by the usual soaking procedures. Prior knowledge of
exactly how Se labels the protein is itself a powerful tool. For example, the
SeMet mutation is an extremely useful amino acid label for fitting a protein
sequence to electron density. Also, noncrystallographic symmetry operators
usually can be defined more reliably from Se positions in SeMet protein than by
heavy-atom positions in conventional derivatives due to the uniformity and
completeness of labeling (Tesmer et al., 1996).
An analogous label is available for nucleic acids in the form of brominated
bases, particularly 5-bromouridine, which is isostructural with thymidine.
Iodinated bases are commonly used as isomorphous derivatives (f0 = 53 e-) for
nucleic acids, but the X-ray edges of I ( = 0.38Å for K,
= 0.38Å for K,
 = 2.56-2.72Å for L) occur at energies less favorable for
accurate macromolecular data collection than does the K edge of Br (
= 2.56-2.72Å for L) occur at energies less favorable for
accurate macromolecular data collection than does the K edge of Br ( = 0.92Å).
= 0.92Å).
Conclusion
Why is the enthusiasm for MAD so high today? There are three primary reasons.
First, cryocrystallography has improved data quality to the point that the
precision required for MAD is usual rather than exceptional. Second, new
synchrotron sources and new beamlines provide intense, reliably tunable X-ray
beams and the instruments to exploit them. Third, MAD works extremely well and
very quickly. For many problems, the experimentally phased electron density is
of stellar quality. Crystallographers are only beginning to appreciate the
value of nearly error-free, model-independent phases (Burling et al.,
1996). The remaining challenges are in two areas. The greatest impediment to
growth of MAD today is access to suitable experimental facilities. This
non-technical problem may be solved only be a concerted effort of the
community. The greatest technical challenge is to develop methods for solving
large partial structures of anomalous scatterers. Here recent results with
statistical direct methods are very promising, and MAD applied to large
macromolecules no longer seems such a heroic undertaking. MAD has at last
taken its place as a standard tool of macromolecular crystallography.
Acknowledgment
Work in the author's laboratory has been supported by grants from the U.S.
National Institutes of Health (DK42303), and from the Lucille P. Markey
Foundation to the Structural Studies Group at Purdue University. Collaboration
with the scientific staffs at synchrotron facilities is gratefully
acknowledged, especially A. W. Thompson of the European Synchrotron Radiation
Facility, and S. E. Ealick of the Cornell High Energy Synchrotron Source.
References
Sorry not yet available
 =
2Å) and 40 keV (
=
2Å) and 40 keV ( = 0.3Å), which give rise to detectable
effects in X-ray scattering from macromolecular specimens labeled with these
elements. Information about the phase of the scattered X-rays can be derived
from the resonance effects, or anomalous scattering. Anomalous scattering is
an atomic property and thus enters the equations for X-ray diffraction in the
expression for the atomic scattering factor (f), which is the sum of "normal"
atomic scattering factor f0 and a complex "anomalous" correction having real
(f') and imaginary (f") components:
= 0.3Å), which give rise to detectable
effects in X-ray scattering from macromolecular specimens labeled with these
elements. Information about the phase of the scattered X-rays can be derived
from the resonance effects, or anomalous scattering. Anomalous scattering is
an atomic property and thus enters the equations for X-ray diffraction in the
expression for the atomic scattering factor (f), which is the sum of "normal"
atomic scattering factor f0 and a complex "anomalous" correction having real
(f') and imaginary (f") components:  T-
T- [2]
[2]

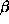 -hydroxydecanoyl thiolester
dehydrase (Leesong et al., 1996). A single methionine amino acid of the
crystalline protein was labeled with Pt by soaking in a solution of K2PtCl4.
-hydroxydecanoyl thiolester
dehydrase (Leesong et al., 1996). A single methionine amino acid of the
crystalline protein was labeled with Pt by soaking in a solution of K2PtCl4. C. Hybrid f" and f' spectra for the Pt LIII edge. Using the program KRAMIG,
the edge region has been cut from the experimental spectrum in B and spliced
into the theoretical spectrum, ua converted to f", and f' calculated from f" by
Kramers-Kronig transformation (Eq. 2).
C. Hybrid f" and f' spectra for the Pt LIII edge. Using the program KRAMIG,
the edge region has been cut from the experimental spectrum in B and spliced
into the theoretical spectrum, ua converted to f", and f' calculated from f" by
Kramers-Kronig transformation (Eq. 2). and
<|F|> =
and
<|F|> =
 for N atoms of identical f (Crick & Magdoff, 1956). The diffraction ratios
of interest to MAD (Hendrickson, 1985) are, for the dispersive signal,
for N atoms of identical f (Crick & Magdoff, 1956). The diffraction ratios
of interest to MAD (Hendrickson, 1985) are, for the dispersive signal, [3]
[3] [4]
[4] [5]
[5]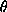 = 0 with
the expressions in Table 2.
= 0 with
the expressions in Table 2.