 . In practice, solution scattering curves decay
rapidly with s and they are normally recorded only at low (not better than 1
nm) resolution, so that the typical number of the Shannon channels does not
exceed 10 to 15.
. In practice, solution scattering curves decay
rapidly with s and they are normally recorded only at low (not better than 1
nm) resolution, so that the typical number of the Shannon channels does not
exceed 10 to 15.
D. I. Svergun
European Molecular Biology Laboratory, Hamburg Outstation, EMBL c/o
DESY,
Notkestrasse 85, D-22603 Hamburg, Germany,
and Institute of Crystallography,
Russian Academy of Sciences, Leninsky pr. 59, 117333 Moscow, Russia.
E-mail:
Svergun@EMBL-Hamburg.DE
 /
/ )sin
)sin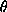 ,
,  is the wavelength, and 2
is the wavelength, and 2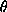 the scattering angle].
Main advantage of solution scattering is the possibility to study the structure
and structural dynamics of native particles in physiological solutions; its
main disadvantage is the loss of information due to the chaotic orientation of
particles.
the scattering angle].
Main advantage of solution scattering is the possibility to study the structure
and structural dynamics of native particles in physiological solutions; its
main disadvantage is the loss of information due to the chaotic orientation of
particles.
Information content in solution scattering data is usually estimated with the
Shannon sampling theorem (Shannon & Weaver, 1949). A scattering curve I(s)
is the Fourier image of the spherically averaged Patterson function of the
particle P(r)=<P(r)> which equals to zero beyond r=Dmax, where
Dmax is the maximum particle size. I(s) is therefore an analytical function.
The sampling theorem states that the number of parameters (Shannon channels)
required to represent an analytical function on an interval [smin, smax] is
equal to Ns= Dmax(smax - smin) /  . In practice, solution scattering curves decay
rapidly with s and they are normally recorded only at low (not better than 1
nm) resolution, so that the typical number of the Shannon channels does not
exceed 10 to 15.
. In practice, solution scattering curves decay
rapidly with s and they are normally recorded only at low (not better than 1
nm) resolution, so that the typical number of the Shannon channels does not
exceed 10 to 15.
In keeping with the low resolution of the solution scattering studies, the data
interpretation is usually performed in terms of homogeneous bodies. Homogeneous
approximation reduces the number of free parameters Np tering is low, an ab
initio shape determination procedure should require as few parameters as
possible. Let us represent the particle envelope by a two dimensional angular
function r=F(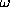 ) describing the particle boundary in spherical coordinates (r,
) describing the particle boundary in spherical coordinates (r,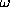 ). This function is conveniently parameterized as
). This function is conveniently parameterized as
 (1)
(1)
where Ylm(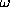 ) are spherical harmonics, the multipole coefficients flm are complex
numbers and the truncation value L defines the resolution of the
representation. The particle density distribution in homogeneous approximation
can be written as
) are spherical harmonics, the multipole coefficients flm are complex
numbers and the truncation value L defines the resolution of the
representation. The particle density distribution in homogeneous approximation
can be written as
(r) =
 (2)
(2)
where 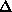 is the width of the particle-solvent interface which for dissolved
macromolecules can be taken
is the width of the particle-solvent interface which for dissolved
macromolecules can be taken 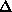 =0.3 nm to account for the first hydration shell.
The particle envelope is thus represented by (L+1)2 numbers flm at a spatial
resolution
=0.3 nm to account for the first hydration shell.
The particle envelope is thus represented by (L+1)2 numbers flm at a spatial
resolution 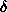 r
r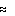
 R0/(L+1), where R0 is the radius of the equivalent sphere.
R0/(L+1), where R0 is the radius of the equivalent sphere.
Solution scattering intensity is I(s) = <I(s)>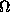 = <{F
[(r)]}2>
= <{F
[(r)]}2>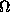 , where F denotes the Fourier transform, <>
, where F denotes the Fourier transform, <>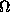 stands for the average over the solid angle
stands for the average over the solid angle 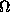 in reciprocal space, and
s=(s,
in reciprocal space, and
s=(s, 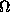 ) is the scattering vector. Expanding
) is the scattering vector. Expanding 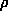 (r) in spherical
harmonics
(r) in spherical
harmonics
 (3)
(3)
the scattering intensity is expressed as (Stuhrmann, 1970a)
 (4)
(4)
where the partial amplitudes Alm(s) are the Hankel transforms from the radial functions
 (5)
(5)
and jl(sr) are the spherical Bessel functions.
Inserting (2-3) into (5) and using the power series expansion for jl(sr) a closed expression for the partial amplitudes via the flm coefficients is obtained allowing one to rapidly evaluate the scattering intensity (4) from a given envelope (Stuhrmann, 1970b; Svergun & Stuhrmann, 1991; Svergun, 1997). Using this approach, an algorithm for ab initio determination of the low resolution envelopes of biopolymers in solution from their experimental scattering curves is developed. Starting from a spherical shape (for which all coefficients but f00 are equal to zero), the flm coefficients are obtained which minimize the discrepancy between the experimental [Iexp(sk), k=1,...N] and calculated curves
 (6)
(6)
with the weighting factor W(sk)= sk2[ (sk)/Iexp(sk)], where
(sk)/Iexp(sk)], where  (sk) is the standard
deviation in the k-th point. Details of the shape determination algorithm are
presented elsewhere (Svergun et al., 1996; 1997a).
(sk) is the standard
deviation in the k-th point. Details of the shape determination algorithm are
presented elsewhere (Svergun et al., 1996; 1997a).
A natural question arises whether the low resolution shape determination is unique, in other words, whether, in addition to the trivial case of an enantiomorphic envelope, different shapes exist at the same level of resolution (i.e. at the same L) yielding identical scattering curves. This problem was considered by Svergun et al. (1996) using computer simulations on model bodies described by the envelope functions exactly represented by a finite series (1) on spherical harmonics. Given the scattering intensity calculated from a model envelope, the particle shape was restored from this intensity with the above algorithm. Both error-free curves and those containing statistical noise were simulated in different angular intervals.
The results indicated that the shape restoration for error-free data is unique,
even when using very limited ranges in the simulated curves. In the presence of
errors, ambiguity of the shape determination depends on the relation between
the number of model parameters Np and that of the Shannon channels Ns. The
shape restoration was found to be practically independent of the initial
approximation and stable with respect to the random errors if Np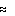 1.5 Ns.
1.5 Ns.
Experimental solution scattering curves cover usually about 10 to 15 Shannon channels thus allowing to use 15 to 20 variables in the shape description. The number of independent parameters in series (1) is equal to Np=(L+1)2-6 (here, the reduction by six variables is due to arbitrary rotations and displacements of the particle which do not alter the scattering curve). It means that in practice the multipole resolution up to L=4 can be used.
Practical implementation of the shape determination algorithm required several extensions to account for the deviations from the ideal model:
(i) When using raw X-ray scattering data, homogeneous approximation may not be valid in the outer parts of the scattering curves where the scattering from the inhomogeneities of the polypeptide chain can no longer be neglected, especially for proteins of low (less than 20kDa) molecular mass. This effect is taken into account as follows. From the inner part of the scattering curve (first three Shannon channels), the best fit three-axial ellipsoid is found. Scattering from the internal inhomogeneities Is(s) inside the ellipsoidal envelope is evaluated using the method of Svergun (1994), and this curve is subtracted from the experimental data so that the difference Iexp(s)- Is(s) at higher angles follows the asymptotic behavior s-4 according to the Porod's law for homogeneous particles (Feigin & Svergun, 1987).
(ii) The model envelope is represented by a finite set of harmonics, whereas real particles would require the infinite series. To reduce the truncation effect, the best fit ellipsoidal envelope is developed into spherical harmonics, and its the shape representation (1) is truncated at the same L value as that used in the shape determination (usually, L=4). The ratio w(s)=IL(s)/Iel(s) is calculated where Iel(s) is the scattering curve from the ellipsoid, IL(s) from its truncated representation. The experimental intensity is then multiplied by this "ellipsoidal filter" w(s) and the resulting curve Jexp(s)= w(s)[Iexp(s)- Is(s)] enters the shape determination.

(iii) When minimizing functional (6), the calculated intensity I(s) at each function evaluation is multiplied by the scaling factor
 (7)
(7)
which provides the currently best least squares fit to the experimental curve. The shape determination can therefore be directly applied to raw experimental data on a relative scale.
The ab initio shape determination program with the above extensions runs on IBM-PC and on major UNIX platforms (Svergun et al., 1997a). Its implementation on a SUN Sparc-20ZX workstation is coupled with a three-dimensional rendering program ASSA allowing the user to monitor the process of the shape determination (Kozin, Volkov & Svergun, 1997).
The program has been tested on several proteins with known atomic structures in the crystal (X-ray solution scattering patterns were collected as parts of ongoing projects at the EMBL Outstation in Hamburg). Figs 1 and 2 present the shape determination of two proteins, monomeric hexokinase and HIV-1 reverse transcriptase (molecular masses 52 and 105 kDa, respectively). In both cases, particle envelopes up to L=4 (19 free parameters) were directly restored from the experimental data starting from a spherical initial approximation. The envelopes are displayed in Fig. 2 along with the atomic structures of the hexokinase (Bennett & Steitz, 1980), and of the reverse transcriptase (Wang et al., 1994) deposited in the Protein Data Bank (Bernstein et al., 1977), entries 1HKG and 3HVT, respectively). As the orientation of the restored models is arbitrary, they and their enantiomorphs were rotated so as to minimize the deviation
 (8)
(8)
where Fcryst(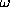 ) is the envelope function evaluated for the atomic structure at
the same L using the program CRYSOL (Svergun, Barberato & Koch, 1995). As
seen from the comparison, the ab initio restoration provides an adequate
low resolution description of the protein envelopes.
) is the envelope function evaluated for the atomic structure at
the same L using the program CRYSOL (Svergun, Barberato & Koch, 1995). As
seen from the comparison, the ab initio restoration provides an adequate
low resolution description of the protein envelopes.
The R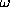 factors are equal to
0.20 and 0.22 for the hexokinase and for the reverse transcriptase,
respectively.
factors are equal to
0.20 and 0.22 for the hexokinase and for the reverse transcriptase,
respectively.

The shape determination program was also used to restore the envelopes of other
proteins with known atomic structures (lysozyme, ribonucleotide reductase,
pyruvate decarboxylase, enopyruvil transferase, etc.). In all these
cases the restored shapes agreed well with the atomic structures, with the R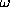 factors ranging from 0.10 to 0.25. Of course, the program is aimed at the shape
determination of the proteins with unknown atomic structure; the above tests
have been done to check the reliability of the method in real experiment.
factors ranging from 0.10 to 0.25. Of course, the program is aimed at the shape
determination of the proteins with unknown atomic structure; the above tests
have been done to check the reliability of the method in real experiment.

Particle symmetry imposes restrictions on the multipole coefficients flm in series (1) and the information about the symmetry, if available, can improve the reliability of the ab initio shape restoration by reducing the number of parameters to be determined. Consider, for example, a homodimeric particle with a two fold symmetry axis along z. In this case, all flm coefficients with odd m vanish, and the particle shape at L=4 is described by 12 independent parameters instead of 19 for a non-symmetric case.
The higher the symmetry, the more multipole coefficients can be omitted, and
this allows one to enhance the resolution of the restoration. Figs 3 and 4
present the shape determination of the homotetramer of pyruvate oxidase
(molecular mass 260 kDa) assuming the 222 point symmetry. The multipole
expansion up to L=6 for this symmetry group requires only 13 free parameters.
The restored envelope displays a good agreement (R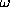 =0.15) with the crystal
structure (Muller & Schultz, 1993, PDB entry 1POW)
=0.15) with the crystal
structure (Muller & Schultz, 1993, PDB entry 1POW)
The quaternary structure of symmetric particles can also be restored in terms
of the envelope function of the asymmetric unit. Thus, scattering from a
symmetric homodimer is readily expressed via the shape of a monomer and
the distance 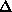 d between the monomers. The shape determination is performed as
described above with a single additional parameter
d between the monomers. The shape determination is performed as
described above with a single additional parameter 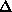 d. This approach has already
been successfully used in practice (Schmidt et al., 1995; Svergun et
al., 1997a).
d. This approach has already
been successfully used in practice (Schmidt et al., 1995; Svergun et
al., 1997a).

The first question to address is why is it at all possible to restore the
three-dimensional envelope from a one-dimensional curve using more parameters
than predicted by the theory? The answer is that the estimate of Ns reflects
only one (and most often quoted) part of the sampling theorem. The other part
says that full information about the entire analytical function is contained in
any finite contiguous portion of it. An oversampled scattering curve measured
with the angular increment much smaller than the sampling distance  /Dmax can be
analytically extrapolated beyond the experimental range (so-called
superresolution). As experimental solution scattering curves are always heavily
oversampled, they are able to provide more parameters than Ns.
/Dmax can be
analytically extrapolated beyond the experimental range (so-called
superresolution). As experimental solution scattering curves are always heavily
oversampled, they are able to provide more parameters than Ns.
Limitations of the model (1) used to describe the particle envelope should be
mentioned. First, as F(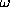 ) is assumed to be single-valued, complicated
(e.g. U-like) shapes or those containing internal holes cannot be
exactly represented. Second, omission of the higher harmonics with l>L is
compensated in the fitting procedure by the artificial enhancement of the lower
ones. This effect is partially corrected by the above described ellipsoidal
filtering and thus produces only marginal distortions for globular particles
but can still be significant for anisometric structures because of a slow
convergence of series (1). Remaining deviations between the restored envelopes
and the crystal structures in Fig. 2 provide an idea on the magnitude of the
truncation effect (it is worth noting that both proteins are rather
anisometric, with the axial ratios of the approximating ellipsoid equal to 2.8
and 3.6 for the hexokinase and reverse transcriptase, respectively).
) is assumed to be single-valued, complicated
(e.g. U-like) shapes or those containing internal holes cannot be
exactly represented. Second, omission of the higher harmonics with l>L is
compensated in the fitting procedure by the artificial enhancement of the lower
ones. This effect is partially corrected by the above described ellipsoidal
filtering and thus produces only marginal distortions for globular particles
but can still be significant for anisometric structures because of a slow
convergence of series (1). Remaining deviations between the restored envelopes
and the crystal structures in Fig. 2 provide an idea on the magnitude of the
truncation effect (it is worth noting that both proteins are rather
anisometric, with the axial ratios of the approximating ellipsoid equal to 2.8
and 3.6 for the hexokinase and reverse transcriptase, respectively).
What is the relation between the solution scattering and crystallographic data? The latter clearly contain more information and provide much higher resolution. However, test runs of the shape determination using simulated reflections instead of solution scattering curves encountered difficulties because of a high multimodality of the goal function. The reason for the multimodality is that the crystallographic data, contrary to the solution scattering curves, are undersampled: separation between the reflections is twice the sampling distance required to describe the three-dimensional scattering intensity as the Fourier image of the density in the unit cell (e.g. Baker, Krukowski & Agard, 1993). Solution scattering data provide therefore complementary information and their use can improve the efficiency of ab initio phasing procedures. Low resolution experimental envelopes can be positioned in the crystal cell using molecular replacement and further refined against both solution scattering and the crystallographic data.
Measurements in solution provide also a possibility to model the structure and structural transitions of complex macromolecules in solution by rigid body movements of their crystallographically known domains (subunits) so as to fit the experimental scattering from the complex (Svergun, 1991; 1994; 1997). Thus, in solution scattering study of the classical allosteric enzyme aspartate transcarbamylase (Svergun et al., 1997), the overall changes accompanying the T->R transition in solution were found to be about 50% larger than those in the crystal (Kantrowitz & Lipscomb, 1988). This approach is now being used in several ongoing projects at the EMBL Outstation in Hamburg to study multidomain proteins in solution.