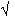 Ihkl). We can see that if we express the electron density as a
Fourier transform of the structure factors:
Ihkl). We can see that if we express the electron density as a
Fourier transform of the structure factors:
Zbigniew Dauter and Peter Main
>Depts. of Chemistry and Physics, University of York, YO1 5DD
The term 'direct methods' is used in small molecule
crystallography to describe methods of structure solution, that is to say
methods for phase derivation, by purely mathematical means utilising the
measured structure amplitudes only. In a diffraction experiment it is only
the structure factor amplitudes |Fhkl| that are measured (|Fhkl| =
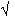 Ihkl). We can see that if we express the electron density as a
Fourier transform of the structure factors:
Ihkl). We can see that if we express the electron density as a
Fourier transform of the structure factors:
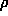 (xyz) =
(xyz) = 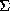 hkl |Fhkl| exp(ijhkl) exp 2
hkl |Fhkl| exp(ijhkl) exp 2 i(hx+ky+lz)
i(hx+ky+lz)
|Fhkl| x exp(ijhkl) = FhklThe Fourier transform of the amplitudes gives a function very similar to the Patterson, which has a huge peak at the origin and does not correspond to the actual electron densityFT FT FT
amplitude * phase =
(xyz) synthesis synthesis (
Patterson)
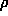 (xyz). Most of the information about positions
of the atoms in the crystal, or peaks in
(xyz). Most of the information about positions
of the atoms in the crystal, or peaks in 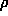 (xyz), must be contained in the
phases of the structure factors. Therefore the fundamental problem in the
crystallographic diffraction analysis is the phase problem.
(xyz), must be contained in the
phases of the structure factors. Therefore the fundamental problem in the
crystallographic diffraction analysis is the phase problem. Several methods of solving the phase problem exist, starting from trial and error modelling for the simplest of the structures, through interpretation of Patterson function with unknown or known (Molecular Replacement) structural models, to rather tedious methods utilising the signal from the heavy atoms either already present in the structure (e.g., MAD) or substituted into the structure (MIR). The term direct methods traditionally refer to methods of phase calculation which utilise analytical mathematical (probabilistic) equations based only on the observed structure factor amplitudes.
The structure factors, i.e. their amplitudes and phases, in general, depend on the distribution of atoms in the unit cell of the crystal:
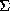 j fj exp(-B/4d2)
exp -2
j fj exp(-B/4d2)
exp -2 i(hxj+kyj+lzj)
i(hxj+kyj+lzj)
The atomic coordinates, xj, yj and zj are expressed as fractions of the cell edges and relate to a common reference point, the origin of the cell. It is convenient to fix the origin at symmetry positions such as a center of symmetry if it exists. In other space groups, such as P21, it may lie on the screw axis anywhere along b direction. Moreover in most space groups there are several special positions of the same symmetry and any of them can be selected as the origin of the cell. Change of the origin will not change the amplitude but in general may change the individual phases. The table shows how the phases (or in this case, signs) of reflections with different parity of their indices change when the origin is shifted between eight possible centres of symmetry in space group P-1.
origin shift 0,0,0 1/2,0,0 0,1/2,0 0,0,1/2 0,1/2,1/2 1/2,0,1/2 1/2,1/2,0 1/2,1/2,1/2 parity eee + + + + + + + +eeo + + + - - - + -
eoe + + - + - + - -
oee + - + + + - - -
eoo + + - - + - - +
oeo + - + - - + - +
ooe + - - + - - + +
ooo + - - - + + + -
In this case only reflections with all three indices even do not change
their phase when the origin is shifted. In the process of ab initio
phase estimation it is necessary to ensure that all phases form a consistent
set and refer to a common origin. Analysis of phase dependence on the selection
of different origins, permissible in given space group, leads to the concept of
structure seminvariants. They are the structure factors or their linear
combinations, whose phase does not depend on the choice of the origin, under
the condition that it is allowed for the particular space group. One of the
simplest seminvariants is formed by a so-called 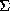 2 triplet of three
structure factors Eh, Ek and E-h-k, for which the sum of indices is zero.
2 triplet of three
structure factors Eh, Ek and E-h-k, for which the sum of indices is zero.
The selection of one of the several possible origins can be done by a free ch! oice of phases for three (or less, for centered or higher symmetry cells) reflections, which do not form seminvariants.
The equation for the electron density does not provide a direct relationship between structure factor amplitudes and phases. If the electron density was completely unknown, the amplitudes and phases would need to be treated as completely independent. Fortunately, we have some expectations about the electron density which indirectly constrain the terms in the right hand side of the electron density equation. Since the amplitudes are known, those constraints can be utilised to formulate some phase restrictions. Many analytical or probabilistic relationships of different strength and usefulness have been proposed. For the pioneering work in this field, setting out the basis of the direct methods, Jerome Karle and Herbert Hauptman were awarded Nobel Prize in Chemistry in1985.
The features of the electron density ! which can be expressed mathematically and used in structure determination are set out here:
1. atomicity of 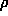 (x) normalised structure factors
(x) normalised structure factors
2. positivity of 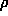 (x) inequalities and determinants
(x) inequalities and determinants
3. equal atoms Sayre's equation
4. 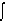
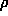 3(x) dV = max. tangent formula
3(x) dV = max. tangent formula
5. -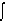
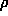 (x) ln
(x) ln 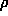 (x) dV = max. maximum entropy methods
(x) dV = max. maximum entropy methods
6. partial structure modification of probability equations
7. multiple motifs molecular replacement
8. 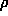 (x) = const. solvent flattening and density modification
(x) = const. solvent flattening and density modification
It is known from the principles of chemistry that the atoms cannot lie closer together than a certain distance. The electrons ar! e concentrated to a certain volume around the atoms and the thermal vibration smears out the electron density to some extent around the average atomic positions, but in general the electron clouds of separate atoms do not overlap considerably. This can be utilised to remove the effect of the atomic or, rather, electron cloud shape (represented by the term fj exp(-B/4d2)) from the structure factor. Removal of the term fj exp(-B/4d2) from the structure factors Fhkl , substituting them by the normalised structure factors, Ehkl leads to the deconvolution of the point atom structure, as can be seen from the following relationship:
Ehkl x fj exp(-B/4d2) = Fhkl
! FT FT FT
point atom * real = 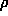 (xyz)
(xyz)
structure atom
This can be done by dividing the structure amplitudes by their average value in the resolution ranges:
|Ehkl|2 = Ihkl / <I>
and can be represented by the Wilson plot (1942) which in average is horizontal. This procedure weights up the high resolution intensities, intrinsically small due to the atomic shape and its vibration and allows the selection of the relatively largest structure factors in all resolution ranges. Direct methods anyway usually utilise only a subset of the largest am! plitudes in the process of phase estimation.
40The electron density must not be negative, otherwise it has no physical meaning. This constraint leads to the formulation of inequality relations, which were the first of the mathematical expressions connecting the phases and amplitudes of the structure factors, given by Harker and Kasper (1948). An example of such inequality in terms of unitary structure factors (Uhkl = Fhkl / F000):
U2hkl <= 1/2 (1 + U2h2k2l)
is valid in P-1. If both Uhkl and U2h2k2l are sufficiently large, the inequality relationship can prove that the sign of U2h2k2l must be positive. Such relationships were generalised by Karle and Hauptman (1950) and also expressed in the form of determinants. However, inequalities are no! t powerful enough and are not used in practice any more.
If we neglect the hydrogens, the assumption that the crystals of organic compounds consists of equal atoms is a good approximation. The diffracting power of carbon, nitrogen and oxygen with 6, 7 and 8 electrons are similar. If we also take into account atomicity of the electron density, it leads to so-called Sayre's equation. This was formulated in three papers published in 1952 by Sayre, Cochran and Zachariasen in the same volume of Acta Cryst.
If the electron density within the crystal consisting of equal atoms is squared, the resulting 'squared' density is almost proportional to the original, except that the atomic peaks have a somewhat different shape. We can introduce the structure factors of the squared structure,
Ghkl! = g 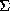 j exp 2
j exp 2 i (hxj+ky0j+lzj) = g/f f
i (hxj+ky0j+lzj) = g/f f 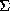 j
exp 2
j
exp 2 i (hxj+kyj+lzj) = g/f Fhkl
i (hxj+kyj+lzj) = g/f Fhkl
On the other hand, from the following convolution
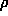 (r) x
(r) x 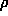 (r) =
(r) = 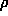 2(r)
2(r)
FT FT FT
Fh * Fh = Gh
it can be shown that Gh = 1/V Fh * Fh = 1/V 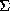 k Fk
F! h-k , and we obtain the Sayre's equation:
k Fk
F! h-k , and we obtain the Sayre's equation:
Fh = 1/V f/g 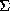 k Fk Fh-k
k Fk Fh-k
which gives exact relationship among the structure factors. It is the most important equation in direct methods and forms the basis of phase propagation and refinement.
Closely related to the Sayre's equation is the tangent formula, given by Cochran (1956), which can be expressed as follows:
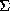 k |Ek Eh-k| sin (jk + jh-k)
k |Ek Eh-k| sin (jk + jh-k)
tan jh = ___________________________________________________
! dctlpar 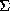 k |Ek Eh-k| cos (jk + jh-k)
k |Ek Eh-k| cos (jk + jh-k)
The tangent formula is based on the probability considerations for the distribution for the unknown phase jh with the other phases known. The reliability of the formula depends on the value of:
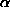 h = 2/
h = 2/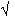 N |Eh| |
N |Eh| | 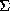 k Ek Eh-k |
k Ek Eh-k |
A simplified conclusion from the tangent formula and Sayre's equation is that
for non-centrosymmetric crystals Eh has phase of { 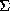 k Eh Ek Eh-k }
k Eh Ek Eh-k }
! and for centrosymmetric crystals Eh has sign of { 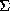 k Eh Ek Eh-k }
k Eh Ek Eh-k }
If the values of all three normalised structure factors of the 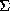 2
triplet are large, there is a high probability that even for a single triplet
their phases sum to zero, or (for centrosymmetric crystals) the product of
their signs is positive. This is the basis of the symbolic addition
procedure, introduced in the early 1960's by Isabella Karle. Symbolic addition
was widely used in the era before automatic programs and fast computers became
available.
2
triplet are large, there is a high probability that even for a single triplet
their phases sum to zero, or (for centrosymmetric crystals) the product of
their signs is positive. This is the basis of the symbolic addition
procedure, introduced in the early 1960's by Isabella Karle. Symbolic addition
was widely used in the era before automatic programs and fast computers became
available.
In this method the phases of some reflections were represented by letter
symbols, and together with the origin fixing reflections constitute the
starting set. In non-centrosymmetric space groups the phase of one more
reflections can be chosen to fix the enantiomorph. Th! e symbols are then
propagated through a number of 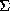 n4 2 relations, so that a number
reflections have phases represented by symbols. Some reflections may have
several different estimations expressed by different symbols, which provides
additional relations between symbols or allows to assign specific phase to a
symbol. The example below illustrates the procedure for P-1 symmetry.
n4 2 relations, so that a number
reflections have phases represented by symbols. Some reflections may have
several different estimations expressed by different symbols, which provides
additional relations between symbols or allows to assign specific phase to a
symbol. The example below illustrates the procedure for P-1 symmetry.
origin fixing reflections: 3 0 2 +
2 -3 2 +
1 2 -1 -
symbols 0 3 3 a
3 2 4 b
phase propagation:
! r 3 0 2 + 3 0 2 +
2 -3 2 + -1 -2 1 -
5 -3 4 + 2 -2 3 -
1 2 -1 - -2 3 -2 +
0 3 3 a 3 2 4 b
tx3969 1 5 2 -a 1 5 2 b
From the last two relations it is evident that b = -a, and the number of symbols can be reduced. This procedure finally leads to a single combination of phases which hopefully provides an interpretable E-map.
In the multisolution approach, introduced in 1970's in York in the program MULTAN (Germain, Main & Woolfson, 1970), the phases of the reflections in the starting set are permuted and those combinations then propagated and refined, thus producing a number of potential solutions. The starting phases can be permuted in a simple way, with centrosymmetric reflections having 0 or 180deg. and non-centrosymmetric ones 45, 135, 225 or 335deg., giving either 2n or 4n combinations. Another method of sampling the phase space more effectively with less permutations is based on the idea of magic integers (White & Woolfson, 1975). The phases of the starting se! t reflections are expressed as a function of a single variable:
ji = mi x mod(2)
for a sequence of mutually prime integer numbers mi.
A variation of the multisolution method, which gained more popularity with the increased availability of faster and larger computers, is the random approach. The random phases can be assigned to the limited phase set, as in the multisolution approach, and then propagated and refined as in the program RANTAN (Yao, 1981), or all phases given the random values and then refined to consistency as in SHELXS (Sheldrick, 1990). The last approach is gaining more popularity lately and is implemented in most of the contemporary direct methods programs.
! rd The multisolution and random methods create a large number of phase sets, some of which are correct, leading to interpretable E-maps, and some incorrect. The identification of the correct set(s) is not easy and requires the use of reliable figures of merit, which test the quality of phases. Several different FOM's have been proposed and used in different programs.
ABSFOM checks the internal consistency of triplets, its value should be 1 for correct set and 0 for random phases. R checks the deviations from the expected values of h. 0 makes use of the triplets with Eh small. Obviously such reflections do not take part in the phase refinement and therefore provide an independent check ! of phase correctness. NQEST is based on negative quartets, for which Eh, Ek, Ek, Eh+k+l are large but Eh+k , Ek+l and El+h are small. The phase of such seminvariant j4 = jh + jk + jl + jh+k+l is expected to be 180deg., therefore NQEST should have a negative value for good phases. In practice often the direct methods programs use a combination of several figures of merit and select the best phase set according to combined figure of merit.
The structure determination by direct methods consists of the following steps:
1. Calculation of normalised structure factors from Fobs and selection of a set of large E's
2. Setting up f1S2 phase relationships, Eh E4 k Eh-k
3. Phase assignment to the starting set, including origin fixing
4. Phase propagation and refinement
5. Calculation of figures of merit
6. Computation and interpretation of the E-map.
In contemporary direct methods programs all these steps can be performed automatically, without manual intervention. Indeed, most of small structures with up to about 100 atoms can be solved using the default program options. This is not the case for larger molecules, including small proteins, for which the process of solving the structure by direct methods is far from routine and requires diffraction data to extend beyond 1.2 Å, involves generation of an enormous number of phase sets and the use of efficient figures of merit. Largest structures solved so far by direct methods have 400 - 500 atoms (Dauter, Lamzin & Wilson, 1995, S! heldrick et al., 1993). Hovever, recently Herbert Hauptman (1996) formulated an optimistic opinion that within 10 years we should be able to solve structures with up to 1000 atoms at somewhat lower resolution.
References
Cochran, W. (1952) Acta Cryst., 5, 65 - 67.
Cochran, W. (1955) Acta Cryst., 8, 473 - 478.
Dauter, Z., Lamzin, V.S. & Wilson, K.S. (1995) Curr. Op. Struct. Biol., 5, 784 - 790.
Harker, D. & Kasper, J.S. (1948) Acta Cryst., 1, 70 - 75.
Hauptman, H. (1996) IUCr Congress, Seattle, Abstract no. BL.01, p. C-7.
Hauptman, H. & Karle, J. (1953) ACA Monograph No. 3, Polycrystal Book Service.
Karle, J. & Hauptman, H. (1950) Acta Cryst., 3, 181 - 187.
Karle, J. & Karle, I.L. (1966) Acta Cryst., 21, 849 - 859.
G! ermain, G., Main, P. & Woolfson, M.M.(1970) Acta Cryst., B26, 274 - 285.
Sayre, D. (1952) Acta Cryst., 5, 60 - 65.
Sheldrick, G.M. (1990) Acta Cryst., A46, 467 - 473.
Sheldrick, G., Dauter, Z., Wilson, K., Hope, H. & Sieker, L. (1993) Acta Cryst., D49, 18 - 23.
White, P.S. & Woolfson, M.M. (1975) Acta Cryst., A31, 53 - 56.
Wilson, A.J.C. (1942) Nature(London), 150, 151.
Yao, J.-X. (1981) Acta Cryst., A37, 642 - 644.
Zachariasen, W.H. (1952) Acta Cryst., 5, 68 - 70.