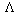( {g} , FP*(h) )
= p( FP*(h) | {g} )
E. de La Fortelle, J. Irwin
MRC Laboratory of Molecular Biology, Hills Road, Cambridge CB2 2QH England
eric@mrc-lmb.cam.ac.uk, ji10@mrc-lmb.cam.ac.uk
http://Lagrange.mrc-lmb.cam.ac.uk
and G. Bricogne
MRC Laboratory of Molecular Biology, Hills Road, Cambridge CB2 2QH England
and LURE, bât 209d, F-91405 Orsay Cedex, France
gb10@mrc-lmb.cam.ac.uk
http://gerard2.mrc-lmb.cam.ac.uk
Abstract
The problem of estimating heavy-atom parameters (esp. occupancies) from acentric reflexions in the MIR method has a long history of difficulties, and a conceptually satisfactory solution allowing bias-free refinement of all parameters (including the lack of isomorphism) has only recently been obtained by a recourse to the method of maximum-likelihood estimation. The situation is essentially identical in the case of MAD phasing. The maximum-likelihood method needs to be invoked to exploit incomplete phase information in a heavy-atom parameter refinement while preventing that information from biasing the results.
We have designed and written from scratch a computer program - SHARP (Statistical Heavy-Atom Refinement and Phasing) - that fully implements the maximum-likelihood approach. It can refine simultaneously scale, a model for the lack of isomorphism and all heavy-atom parameters from MIR and MAD data, or any mixture of them. The program has been systematically tested, both on synthetic and on measured data, and compared to MLPHARE. The results show the superiority of our approach, especially in cases of low signal-to-noise ratio. The likelihood function has also been used as a detection tool to plot residual Fourier maps and probe for minor sites, and for the calculation of phase probability distributions encoded in Hendrickson-Lattman coefficients.
At the same time as the first attempts were being made to use phase estimates, an alternative refinement scheme was devised by Rossmann [7], based on a difference-Patterson correlation criterion, and evolved towards the "FHLE method" [8],[9], and finally the "origin-removed Patterson-correlation function" [10]. Here the use of acentric phase estimates is avoided altogether, but at the price of impoverishing the available information in the sense that multiple derivatives are not allowed to assist each other's refinement through the generation of phase information.
Sygusch [11] recognized that a middle-ground could perhaps be found if the acentric phases were no longer deemed to be "estimates", but were instead treated as extra parameters and refined along with the others. Unfortunately, the enormous increase in the number of variables dictated the use of a diagonal approximation, which rather defeated the original purpose of accommodating the correlations between phases and parameters. Bricogne [12], [13] proposed a solution that partially overcame these difficulties. The main idea was that structure-factor estimates for acentric reflexions are implicit functions of the parameters that are being refined. This dependence was shown to result (via the chain rule) in a correction to the partial derivatives from which the normal equations of the least-squares method are to be formed. Many previously observed pathologies, such as the rapid divergence of the site occupancies of good derivatives, were cured by this analysis, but slower-moving instabilities were observed that resulted in divergent behaviour of the estimates for the lack of isomorphism of the various derivatives. Moreover, the problem of bimodality remained.
At this point, compliance with the first cardinal rule of the least-squares method had been essentially restored, but attention was drawn to the violation of a second cardinal rule : the inverse-variance 'weights' in the expression for the least-squares residual should be kept fixed as if they were part of the observed data. Since the method of least-squares is a special case of the maximum-likelihood method when errors are normally distributed with fixed (co)variances, it is clear that the problem of properly estimating the lack-of-isomorphism parameters demanded a fully-fledged maximum-likelihood treatment rather than least-squares.
Perusal of the literature shows that two-dimensional statistical 'phasing' (probability distribution on the phase and on the modulus of the native structure factor) had been considered as early as 1970 [14], leading to the first mention of likelihood in this context by Einsein [15]. The first mention of parameter estimation by maximum-likelihood, in a very limited context, is found in Green [16]. Maximum-likelihood (ML) refinement for heavy-atom parameters was then advocated by Bricogne [17],[18],[19], Read [20], and an approximation to it was implemented by Otwinowski [21] in the program MLPHARE. This program is only a partial implementation of ML refinement - best described as 'phase-integrated least-squares' - in the sense that (i) it integrates the exponential of the least-squares residual and its partial derivatives only over the phase of the native structure factor (not over its modulus) ; and that (ii) the lack of isomorphism is still re-estimated at the end of each refinement cycle rather than being refined, and may often converge to non-optimal values. Nevertheless, this approach has been shown in numerous cases to yield better results than earlier refinements, drawing attention to the potential of maximum-likelihood methods.
The maximum-likelihood formalism outlined in Bricogne [22] for the MIR and SIR cases forms the basis of the present work. We will describe here its extension to probability distributions incorporating anomalous diffraction effects as well as measurement error and non-isomorphism. Integrating these distributions in the whole complex plane leads to likelihood functions that can be used for heavy-atom detection and refinement, and for producing phase probability distributions. We will also describe the current implementation of this formalism in a computer program, named SHARP (for Statistical Heavy-Atom Refinement and Phasing) [23].
More specifically, a least-squares (LS) model is always formulated as a prescription for turning given values of model parameters into 'calculated' (error-free) values to be compared with the observables. Error estimates are obtained a posteriori, by examining the residual discrepancy between the 'calculated' and the 'observed' quantities. By contrast, a likelihood-based model casts its predictions directly in the form of probability distributions for the observables, the quantities called 'calculated' in the LS formalism usually appearing as parameters in these distributions.
For a centric reflexion, the probablity distribution becomes one-dimensional, but the theory is essentially similar.
This probability distribution is then transformed into a likelihood distribution for that reflexion, via the simple rule (in the absence of prior phase information) :
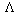( {g} , FP*(h) )
= p( FP*(h) | {g} )
Note that this equation is valid at each trial point FP*(h) in the Harker plane. In order to have a likelihood function that is independent of assumptions on the native complex structure factor, we must now integrate the likelihood function over all possible values of FP*(h) :
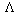( {g} ) =
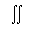
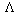( {g} , FP*(h) )
d2FP*)
In the case of a centric reflexion, the integration is one-dimensional only, along the axis defined by the centric phase.
Future developments will incorporate a parametrisation of the anisotropy of anomalous scattering [24],[25] and will allow a refinement of the corresponding parameters from unmerged data carrying suitable goniometric information for each measurement.
kj(h) = Kscj exp[-1/4
B(scj)(d*)2)
exp[-(
bp,qjhphq)]
This error can be broken down in three main components :
* The measurement error, that is part of the crystallographic data and not refined.
* The physical lack-of-isomorphism error.
In the absence of structural evidence for 'localised' lack-of-isomorphism, our assumption will be that of Luzzati [26] that there is a random isotropic positional perturbation, with spatially uniform mean amplitude and normal distribution, over the whole asymmetric unit. Based on this hypothesis, following the work of Read [27] and Dumas [28], we used a one-parameter model for the physical lack-of-isomorphism variance, increasing with resolution.
* The model error.
This error has the same effect on the statistical distribution of the native structure factor as the previous one, but its variance is approximately decreasing with resolution as the mean intensity of remaining heavy atoms. We used a two-parameter model (a constant and a temperature factor) for this error.
A similar parametrisation is used for the error on the anomalous differences. Although there is no physical basis for adopting the same model, it was thought flexible enough as a function of resolution to fit to more diverse functions of resolution.
These maps enable the detection of minor sites, and perform this task in an optimal fashion because they take into account the full unbiased phase information available from the data at the current stage of refinement. They are essentially Fourier syntheses calculated from inverse-variance weighted difference coefficients between the derivative and native data. Their enhanced sensitivity to any departure from the current heavy-atom model (when the data are accurate enough, and to high enough resolution) makes them the instrument of choice to detect more subtle features, such as anisotropy in the heavy-atom temperature factors or structural disorder at certain sites.
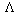(FP*,{g}) considered as a
function of the trial native structure factor FP* only,
becomes (after suitable normalisation) the probability distribution function of
the modulus and phase of the native structure factor (this is a simple
application of Bayes's theorem). The two-dimensional centroids
FPbest(h), used as Fourier coefficients of the
electron-density map, and the Hendrickson-Lattman 'ABCD' coefficients
[29] of
the marginal phase distribution can be easily derived from this likelihood
function.
In order to offer ab initio detection capability, another type of map will be added to the existing program. Its coefficients will initially involve second-order derivatives of the log-likelihood function associated to the null hypothesis defined by "all intensity differences between data sets are caused by lack of isomorphism". This map will have the character of a Buerger sum function over a weighted difference-Patterson function [30]. As major sites are detected and included in the substitution model, the log-likelihood function will develop first-order derivatives giving rise to a difference-Fourier component in the residual map, while the revised second-order derivatives will keep contributing a component with the character of a sum function over a residual difference-Patterson.
The whole process of detecting sites and of assessing their significance quantitatively can thus be automated, using the log-likelihood gain referred to the null hypothesis as a scoring criterion for the peak-search. The procedure will stop when the highest remaining peak in the residual maps is essentially at the level of the noise.
Once all heavy atoms have been detected and refined, the remaining features in the 'isomorphous' residual maps, if they are significant, can provide the basis for a systematic study of lack of isomorphism. This could improve the rather crude way in which 'global' and 'local' lack of isomorphism have hitherto been described.
The result is a forms-based interface, written in HTML language and processed by Perl scripts, that exactly mirrors the hierarchy of parameters during the buildup of the parameters file, and that connects automatically to Graphical Helper Applications to facilitate inspection of the output.
In the same way, the documentation can be accessed in a context-sensitive manner by clicking on hyperlinks called 'explanation', scattered at all points of interest in the master file and in secondary details files.
Graphical applications are triggered through a Unix "mailcap" mechanism, that relies on the extension of a file name to determine what program to use for visualising the contents. All statistics relative to the data (histograms of intensity, of isomorphous and anomalous differences) and to the phasing (lack of isomorphism statistics, phasing power and Rcullis) can be visualised that way, and maps can be plotted in programs npo [31] or O [32] by pressing a button in the interface, without having to program specific instructions for these graphical tools.
The starting heavy-atom model consisted in two selenium atoms with isotropic
thermal motion. Refinement of this model showed that, consistently with the
results of other refinement procedures, the second selenium atom had a high
temperature factor (around 60). Once the refinement was completed, the residual
maps showed strong anisotropic features for the first selenium site and weaker
anisotropy for the second. We consequently updated the heavy-atom model by
allowing an anisotropic temperature factor for both seleniums atoms. The
resulting residual map showed much less features above the noise level, except
for a 10
peak at 1.8 Å distance from the first selenium site.
The second update of the heavy-atom model allowed for a third selenium atom
with an isotropic temperature factor, that refined to a low occupancy (0.2).
The remarkable result was that the added occupancies of site 1 and site 3 were
equal to the the occupancy of site 2 within the standard deviation of this
parameter. This observation, added to the small distance between site 1 and
site 3, shows that this methionine residue has a double conformation.
We then used the density modification program SOLOMON [35] to improve the phases, assuming that it would yield better results when the input phase probability distributions (encoded as Hendrickson-Lattman coefficients) are statistically more accurate. The density modification prodedure for both SHARP and MLPHARE was exactly similar. The results are summarized in Table 1.
The starting heavy-atom model consisted of two mercury sites, for which coordinates, occupancy and temperature factor were determined in a first round of refinement. The residual map plotted at the end of this refinement showed strong anisotropy features for both sites, and a suspicion of a double position for site 1. The anisotropy was refined first, and the subsequent residual map clearly showed that the cysteine residue to which the first mercury was bound had a double conformation. Once this was taken into account in the heavy-atom model in a third round of refinement, the residual map showed no more significant features, thus proving that the refinement was complete. The resulting map, after density modification in SOLOMON, was of high quality (see Table 2).
Interestingly, in this case the anomalous residual map yielded a much clearer information that the isomorphous redsidual map. This was confirmed by the phasing power statistics, which showed that, due to significant lack of isomorphism, the anomalous signal contributed far more to the phasing than the isomorphous signal. The whole procedure of refinement and phasing was then started again from the same initial assumptions, but without using the native data. Heavy-atom refinement yielded the same results, and the residual maps allowed unambiguous detection of both the anisotropic thermal motion and the double conformation. Phasing of this "Single-Wavelength Anomalous" dataset, followed by the same solvent-flattening procedure, yielded an interpretable electron-density map, although of a lesser quality than the SIRAS map (see Table 2).
The test of using the anomalous scattering of a derivative by itself, in the second example, is of special interest. It was not useful for the determination of the structure in that particular case because the isomorphism was relatively good between the native and mercury derivative crystals. It shows nonetheless that, in cases of very strong non-isomorphism, a well-substituted derivative can be used by itself to provide phase information, if the anomalous signal is strong. In such a case of complete bimodality in the phase distribution of acentric reflexions, the main purpose of the density modification procedure is to select the right mode. SOLOMON seems to perform this task for most reflexions thanks to the envelope constraints.
[3] R.G. Hart Acta Cryst. 14, pp.1194-1195, 1961.
[22] G. Bricogne op. cit, 1991.
[24] D.H. Templeton & L.K. Templeton Acta Cryst. A38, 62-67, 1982.
[25] L.K. Templeton & D.H. Templeton Acta Cryst. A44, 1045-1051, 1988.
[26] V. Luzzati Acta Cryst. 5, 802-810, 1952.
[36] S. Price & K. Nagai, unpublished results.
Glossary :
FOM is the mean figure of merit in that resolution bin.
DELTAPHI is the mean phase difference, weighted by amplitude and FOM,
in that resolution bin.
CORREL is a reciprocal-space correlation coefficient between complex structure
factors. By Parseval's theorem it is equivalent to a real-space correlation coefficient
in that resolution bin.
Resolution ALL 50.0 5.25 3.73 3.05 2.64 2.36 2.16 2.00 1.87 (Å)
SHARP refinement and phasing, density modification with SOLOMON
FOM 0.90 0.84 0.91 0.91 0.90 0.90 0.90 0.90 0.89
<DELTAPHI> 30.5 39.1 25.3 29.5 32.0 30.6 29.3 30.9 32.2
CORREL 0.80 0.70 0.86 0.81 0.77 0.80 0.82 0.80 0.78
MLPHARE refinement and phasing, density modification with SOLOMON
FOM 0.90 0.84 0.91 0.91 0.90 0.90 0.90 0.90 0.89
<DELTAPHI> 30.5 39.1 25.3 29.5 32.0 30.6 29.3 30.9 32.2
CORREL 0.80 0.70 0.86 0.81 0.77 0.80 0.82 0.80 0.78
Table 1 : Quality of IF3-C MAD phasing, in comparison with the refined model
Resolution ALL 50.0 7.83 5.57 4.56 3.95 3.54 3.23 2.99 2.80 (Å)
SHARP refinement and phasing, density modification with SOLOMON - SIRAS data
FOM 0.90 0.89 0.95 0.96 0.96 0.95 0.92 0.89 0.78
<DELTAPHI> 43.3 38.9 35.9 32.6 36.8 42.6 50.8 57.8 64.6
CORREL 0.66 0.64 0.74 0.78 0.73 0.66 0.55 0.46 0.37
SHARP refinement and phasing, density modification with SOLOMON - SAD data
FOM 0.90 0.86 0.93 0.95 0.94 0.95 0.92 0.88 0.82
<DELTAPHI> 57.0 58.2 50.0 48.2 50.7 55.8 62.9 68.0 72.2
CORREL 0.49 0.45 0.57 0.60 0.56 0.49 0.39 0.32 0.26
Table 2 : Quality of U2 SIRAS phasing and SAD (Single-Wavelength Anomalous
Diffraction) phasing, with SHARP