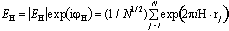Abstract. Shake-and-Bake is a direct methods procedure which has provided ab initio solutions for protein structures containing as many as 600 independent non-H atoms, provided that good-quality diffraction data are available to 1.1Å resolution. Its ultimate potential is unknown. The Shake-and-Bake algorithm extends the range of conventional direct methods by repetitively, unconditionally, and automatically alternating reciprocal-space phase refinement with filtering in real space to impose constraints. An extensive web site for SnB, a computer program implementing Shake-and-Bake, can be found at URL http://www.hwi.buffalo.edu/SnB.

The majority of small-molecule organic crystal structures having fewer than 100 independent non-H atoms are solved using reciprocal-space direct methods. Conventional direct methods begin to fail in the 100-200 atom range because the accuracy of the underlying probabilistic phase relationships decreases as the size of the structure increases. Fortunately, however, the size of molecular structures amenable to phasing by direct methods can be increased significantly if these methods are augmented by the imposition of physically-meaningful constraints in real space. Real-space phase-improvement methods, commonly known as density-modification methods, are widely used in macromolecular crystallography (see review by Podjarny et al., 1987). The potential for real-space constraints to improve phases in the context of small-molecule direct methods was recognized by Jerome Karle (1968) who found that even a relatively small, chemically-sensible fragment extracted by manual interpretation of an electron density map could be parlayed into a complete solution by transformation back to reciprocal space and then performing additional iterations of phase refinement. The tremendous increases in computer speed in recent years have made it feasible to consider repeatedly cycling many trial structures back-and-forth between real and reciprocal space, while performing optimization alternately in each space. This compute-intensive process, which requires the use of two Fourier transforms during each cycle, forms the basis of the synergistic Shake (phase refinement) and Bake (density modification) procedure in which the power of reciprocal-space phase refinement is automatically augmented by filtering to impose the phase constraints implicit in real space (Weeks et al., 1994).

Getting Started. Practitioners of conventional direct methods handle the problem of beginning a structure determination when no atomic positions are known by adopting a 'multisolution' approach in which multiple sets of trial phases are evaluated either symbolically (Karle & Karle, 1966) or numerically (Germain & Woolfson, 1968), with probable correct set(s) determined by ranking according to a suitable figure-of-merit. Since solving very large structures requires a large initial set of presumed-known phases, it has been found advantageous to generate trial phase sets by using a random-number generator to assign values to many or all of the required phases (Baggio et al., 1978: Yao, 1981). In the Shake-and-Bake procedure, phases are assigned initial values by generating trial structures consisting of randomly positioned atoms (thereby imposing an atomicity constraint from the outset) and then computing structure factors.

Foundations of Phase Refinement. Direct methods are based on the fact that there exist linear combinations of phases, called structure invariants, whose values, in principle, depend only on the magnitudes of the normalized structure factors,

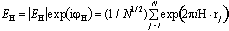(1)

(2)

which have the associated parameters (or weights),

(3)

Ab initio phase determination involves the derivation of individual phase values from a set of triplets having a sufficiently large triplet:phase ratio (e.g., 10:1). The tangent formula,

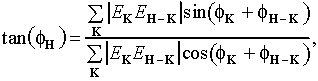(4)

Minimal Function. Minimization of an objective function like the minimal function,

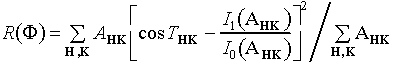(5)

(Debaerdemaeker & Woolfson, 1983; Hauptman, 1991; DeTitta et al., 1994) provides an alternative approach to phase refinement. R() is a measure of the mean-square difference between the values of the triplets calculated using a particular set of phases and their expected values as given by the ratio of modified Bessel functions, and it is expected to have a constrained global minimum when the phases are equal to their correct values for some choice of origin and enantiomorph (the minimal principle). Equation (5) can also be written to include contributions from higher-order (quartet) invariants, but this option has not been shown, within the context of SnB, to be computationally efficient. Experimentation has thus far confirmed that, when the minimal function is used actively in the phasing process and solutions are produced, the final trial structure corresponding to the smallest value of R() is a solution. Therefore, R() is also an extremely useful figure-of-merit.

Parameter Shift. Parameter shift (Bhuiya & Stanley, 1963) is a seemingly simple search technique that has proven to be quite powerful as an optimization method when used to reduce the value of the minimal function, provided that appropriate choices of parameter values are made. The phases are considered in decreasing order with respect to the values of the associated 's. When considering a given phase i , the value of the minimal function (Eq. (5)) is initially evaluated three times. First, with the given set of phase assignments, second with phase i modified by the addition of the predetermined phase shift, and third with i modified by the subtraction of the predetermined phase shift. If the first evaluation yields the minimum of these three values of the minimal function, then consideration of i is complete, and parameter shift proceeds to i +1. Otherwise, the direction of search is determined by the modification that yields the minimum value, and the phase is updated to reflect that modification. In this case, phase i continues to be updated by the predetermined phase shift in the direction just determined so long as the value of the minimal function is reduced, though there is a user-defined predetermined maximum number of times that the shift is attempted. Based on extensive experimentation with these and related parameters, involving a variety of structures in several space groups, it has been determined that in terms of running time and percentage of trial structures that produce a solution, an excellent choice of parameters consists of the following: (i) perform a small number of passes through the phase set, (ii) evaluate the phases in order by decreasing -values, and (iii) for each phase, perform a maximum of two 90° phase shifts. When the parameter-shift phase refinement is applied in centrosymmetric space groups, only a single shift of 180° is required for each phase. Surprisingly, higher success rates have been obtained if restricted phases in acentric space groups are treated as general phases (Weeks et al., 1994).

Real-Space Constraints. Automatic real-space electron-density map interpretation in the Shake-and-Bake procedure consists of selecting an appropriate number of the largest peaks (typically equal to or less than the expected number of atoms) to be used as an updated trial structure without regard to chemical constraints other than a minimum allowed distance between atoms. If markedly unequal atoms are present, appropriate numbers of peaks (atoms) can be weighted by the proper atomic numbers during transformation back to reciprocal space. Thus, a priori knowledge concerning the chemical composition of the crystal is utilized, but no knowledge of constitution is required or used during peak selection. It is useful to think of peak picking in this context as simply an extreme form of density modification appropriate when atomic-resolution data are available. The entire dual-space refinement procedure is repeated for an appropriate number of cycles which have been determined empirically by experimentation with known datasets (Weeks et al., 1994).

The Shake-and-Bake procedure has been implemented in an efficient and easy-to-use program, SnB (Miller et al, 1994). Pertinent information concerning SnB including the complete User's Manual may be accessed from the home page on the World Wide Web at URL:http://www.hwi.buffalo.edu/SnB. Stand-alone UNIX executables for SGI, SUN, IBM, and DEC alpha workstations as well as PC/Linux versions may be downloaded without cost to academic users. SnB has also been incorporated into Molecular Structure Corporation's teXsan package of crystallographic programs, and supercomputer versions have been installed on the Cray T3D and Cray C90 at the Pittsburgh Supercomputing Center, the CM-5 at NCSA, and the SP2 at the Cornell Theory Center.

Overview of the SnB Program. The main menu of SnB gives the user the options of (i) generating and processing trial structures to determine a structure, (ii) producing a histogram of R() values for completed trial structures of a previously submitted structure-determination process, and (iii) displaying the best current trial structure (i.e., lowest R()). A typical application of SnB consists of submitting a structure-determination process, monitoring the progress of the trial structures by occasionally viewing a histogram of final minimal-function values and, when a potential solution is identified, examining the geometry of this structure. The running time of the structure-determination procedure for large, difficult structures requiring many trials is substantial, and the ability to follow conveniently the course of such jobs is essential.

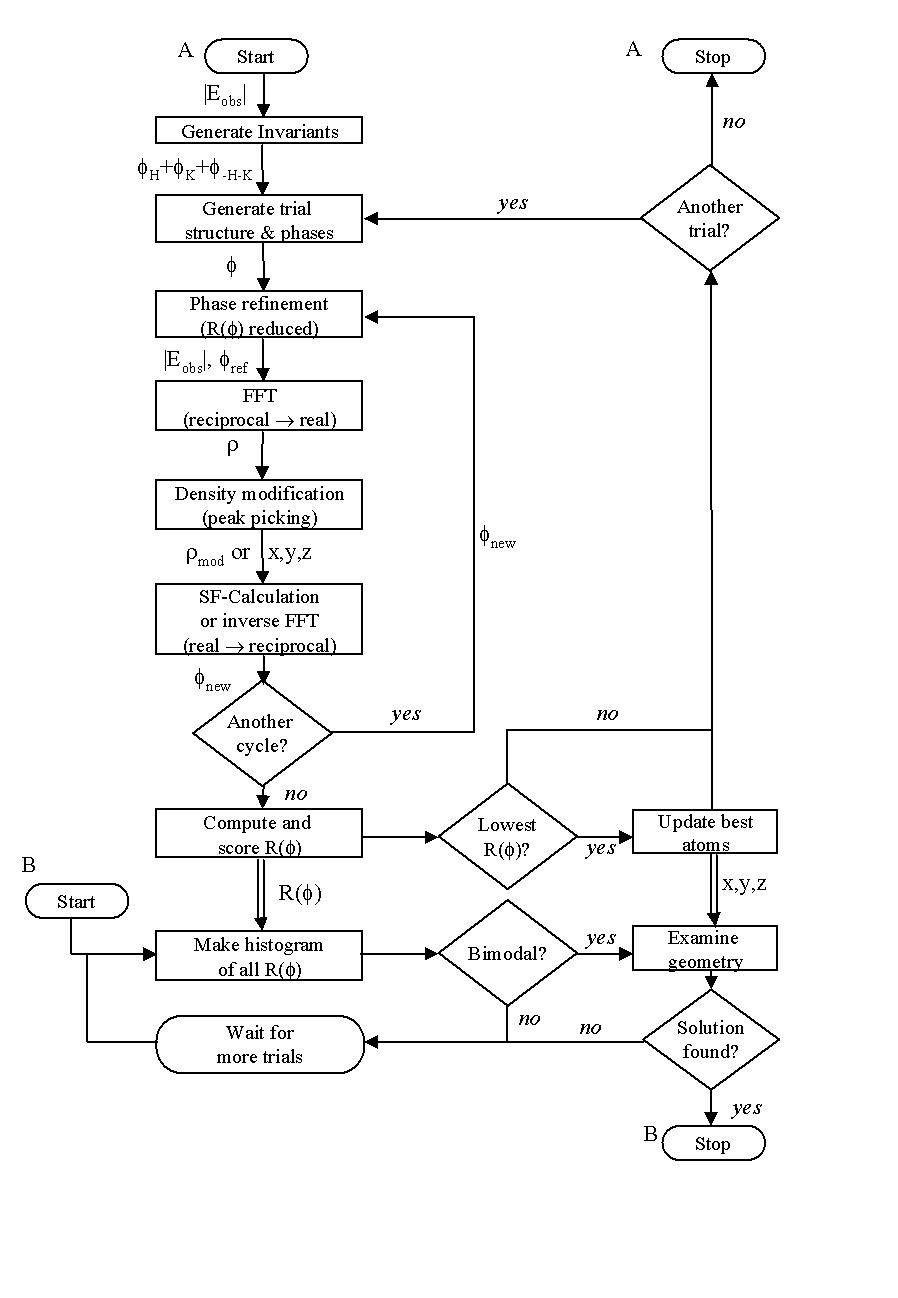
 Figure 1. A flow chart for the Shake-and-Bake algorithm. Solid lines represent flow of control; double lines show movement of data. ‘Start A’ represents the beginning of a structure-determination process, and ‘Start B’ indicates the beginning of a session in which the R() histogram and molecular geometry are checked.

as well as the initial coordinates for the trial structures, are generated. Once this information is available, every trial structure is subjected to the following Shake-and-Bake procedure. Initially, a structure-factor calculation is performed which yields phases corresponding to the trial structure. The associated value of the minimal function, R(), is then computed. At this point, the cyclical Shake-and-Bake phasing procedure is initiated, as follows. The phases are refined via the tangent formula or by parameter shift so as to reduce the value of R(). These phases are then passed to a Fourier routine which produces an electron-density map, but no graphical output is produced. Instead, the map is examined by a peak-picking routine which typically finds the n largest peaks (where n is the number of independent non-H atoms in the asymmetric unit) subject to the constraint that no two peaks are closer than a specified distance. These peaks are then considered to be atoms, and the process of structure-factor calculation, phase refinement, and density modification via peak selection is repeated for the predetermined number of Shake-and-Bake cycles.

For each completed trial structure, the final value of the minimal function is stored in a file, and the histogram routine can be run to determine whether or not a solution appears to be present in the set of completed trial structures. A bimodal distribution with significant separation is a typical indication that solutions are present (as shown in Figure 2), while a unimodal, bell-shaped distribution (e.g., Figure 2 with the ‘0.467 to 0.470’ row omitted) typically indicates a set of nonsolutions. Two options permit the user to view the current best structure. The first requires only a character-based terminal and produces a text plot suitable for printing on a line printer. The user can then manually ‘connect the dots.’ This routine also produces a list of the interpeak distances and angles. The second option makes use of GeomView, a graphical routine developed by the Geometry Center (Center for the Computation and Visualization of Geometric Structures at the University of Minnesota) and suitable for an X-Windows environment. These options are included to assist the user in deciding whether a solution has, in fact, been obtained. They are not intended to provide complete visualization, especially for larger structures. It is expected that the coordinates will be input into other graphical programs for more extensive display.

A few comments concerning the parameters affecting the trial structures are in order. In practice, it is not necessary to use more than 100 randomly positioned atoms as an initial trial structure. During later cycles, choosing n peaks to recycle through the procedure gives optimum success rates for smaller structures. However, for large structures containing a significant number of atoms with low occupancy or high thermal motion, trial structures composed of less than n peaks (e.g., 0.8*n) give better performance. The geometry of trials that are solutions can be improved by E-Fourier recycling (Sheldrick, 1985), and the user can select the number of such Fourier refinement cycles (i.e., SnB cycles with no phase refinement) and the number of peaks. Also, it is often useful to build, over the course of several cycles, from the number of peaks used during the Shake-and-Bake stage to the approximate total number of atoms expected in the structure. When atoms with atomic numbers greater than 10 are present, the user has the option of weighting the appropriate number of largest peaks in the structure-factor calculations. Unequal weighting has resulted in accelerated convergence to solution in cases where a small number of sulfur, iron, or chlorine atoms is present.

Figure 2. A 20-bucket histogram of the final minimal function values after 255 cycles for the 624-atom Tox II structure. 5000 phases and 50,000 triplet invariants were used. The separation between the single solution and the 1618 non-solutions is clearly shown.

The relative efficiency of tangent-formula and parameter-shift phase refinement in Shake-and-Bake has been compared using known atomic-resolution datasets (Weeks et al., 1997). In the case of tangent refinement the minimal function is also computed, but used only as a figure-of-merit. Regardless of which refinement method is used, optimization proceeds most rapidly when there is immediate feedback of each refined phase value. In general, the tangent formula solves small structures (<100 atoms) more cost-effectively, but the two phase-refinement methods are equally efficient for solving most of the tested structures with more than 100 independent atoms, including crambin. However, only parameter shift has produced recognizable solutions for gramicidin A although another figure-of-merit might be more reliable for tangent refinement. In addition, tangent-formula cost-effectiveness is highly dependent on the number of phase-refinement iterations (i.e., the number of passes through the list of phases) per complete Shake-and-Bake cycle whereas parameter shift does not exhibit such strong dependency. The number of iterations per cycle must be chosen judiciously if high efficiency is, in fact, to be achieved. This is especially true for structures in space group P1 where it is never advisable to perform more than one iteration of tangent refinement per cycle. Given a fixed number of machine cycles, it is important to consider the trade-off between the number of trial structures processed and the number of cycles processed per trial structure. Experimentation has shown that, with a phase-refinement technique consisting of a single-iteration, two-step parameter shift of 90°, the point of diminishing returns is at approximately n/2 cycles. Therefore, the program defaults the number of cycles per trial to approximately this value. Overall recommendations for phase-refinement are given in Table 2.

After the dialogue is complete, the user is asked to review the information supplied and make any necessary changes. This information is then stored for use at a later time and for

Table 2. Phase-Refinement Recommendations.

use by the histogram routine. Once a user decides that the parameters are satisfactory, the program automatically initiates the structure-determination procedure by spawning a batch job.

A list of successful SnB applications to protein structures is given in Table 3. Gramicidin A, crambin, and rubredoxin were previously known test structures re-solved at the Hauptman-Woodward Institute. The 64-residue scorpion toxin (Tox II) had been previously solved, but the number of residues and the amino acid sequence were deliberately withheld from the Buffalo group. The only information supplied was that the protein was composed of approximately 500 atoms and contained four disulfide bonds. The remaining structures (vancomycin, Er-1 pheromone, and alpha-1 peptide) were previously unknown, and these applications were made in other laboratories without direct involvement by the authors of SnB. All were solved routinely and automatically using essentially default parameters. Success rate (percentage of trial structures going to solution) depends on size and complexity of the structure, resolution and quality of data, the presence of heavier atoms (e.g., S, Cl, Fe), and the space group as well as the number of refinement cycles. Success rate typically decreases as the size of the structure increases or the resolution or data quality decreases. Success rates for structures in P1 are significantly higher than for other space groups, a result which may be related to the fact that the origin position can be chosen arbitrarily in P1.

The application to Tox II was made on a network of SGI R4000 Indigo Workstations with SnB running as a background job for approximately six weeks. One morning, the histogram reproduced in Figure 2 was found during the daily progress check. After detecting that the histogram was now bimodal, the single trial in the 0.467 to 0.470 range was examined, and a conservative model consisting of five fragments and a total of 241 atoms was constructed. Following multiple cycles of Xplor refinement, the residual was 0.16 for 624 non-H atoms (Smith et al., 1996).

It has been known for some time that conventional direct methods can be a valuable tool for locating the positions of heavy atoms using isomorphous E's (Wilson, 1978) and anomalous scatterers using anomalous E's (Mukherjee et al., 1989). Thus, it is no surprise that the Shake-and-Bake algorithm can be fruitfully applied in this arena as well. The first application of this type was to native and Se-Met data for avian sarcoma virus integrase (Bujacz et al., 1995). The four Se atoms were found using 189 ∆E values (>1.76) in the resolution range 20 to 3.7Å. The investigators report that the isomorphous difference Patterson map was impossible to deconvolute without the aid of direct methods.

The ultimate potential of the Shake-and-Bake approach to the ab initio structure determination of macromolecules is unknown. The combination of this technique with increasingly more-powerful computers has recently permitted direct-method solutions in situations regarded as impossible only a few years ago. The combination of Shake-and-Bake methodology with alternative density-modification methods and supplemental phasing information from isomorphous replacement and single or multiple-wavelength anomalous dispersion may allow equally spectacular advances in the near future.

Table 3. Protein structures solved ab initio by SnB

Acknowledgments. The Shake-and-Bake algorithm and the SnB program have been made possible by the financial support of grants GM-46733 from NIH and IRI-9412415 from NSF. The authors would like to acknowledge the guidance and inspiration provided by Prof. Herbert Hauptman throughout the development of SnB.