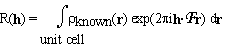. (2.1)Abraham Szoke, Hanna Szoke
First, we have to explain why our method is called holographic. Let us start from the analogy of an X-ray diffraction pattern and a hologram. We assume, maybe artificially, that we know the electron density in part of the unit cell of a crystal. This is the situation in molecular replacement and also during the solution of crystal structures. The complex amplitude of the wave diffracted from the known part can then be calculated and identified as a holographic reference wave. Similarly, the wave diffracted from the unknown part of the unit cell is analogous to an object wave in holography. The pattern of intensities observed in X-ray diffraction from a crystal is then analogous to a recorded hologram. It contains the sum of the intensities of the waves scattered from the known and the unknown parts of the electron density of the crystal and also their interference. The interference term contains phase information that can in turn be used to find the unknown part of the electron density. In the language of holography the unknown wave can be reconstructed and its source can be found. We show below that the reconstruction reduces to a standard inverse problem, similar to those encountered in image processing. Our algorithm, built on the above observations, searches in real space for an electron density that minimizes the deviation of the magnitudes of the calculated structure factors from the measured ones. We have found that the ubiquitous holographic "dual image" also appears in X-ray crystallography, in fact it is equivalent to the phase problem of crystallography. Under favorable conditions, additional information can eliminate the dual image.
A practical algorithm for X-ray crystallography was developed by recognizing that the holographic method can use fast Fourier transforms and a conjugate gradient optimizer, that is capable of incorporating various constraints. The result was a suite of computer programs (EDEN, for Electron DENsity) for the solution of crystallographic problems of current interest. The main solver program runs in PlogP time, where P is the total number of resolution elements in the unit cell. Work stations (IBM 6000, HP 9000, SGI Iris, or equivalents) are adequate for treating realistic problems. Our progress was documented in five published papers [Szoke (1993, paper II), Maalouf et al., (1993, paper III) and Somoza et al. (1995, paper IV), Szoke, Szoke & Somoza (1997, paper V) also Beran & Szoke (1995)]. EDEN is available free of charge to qualified collaborators. Please contact H. S. by e-mail at szoke2@llnl.gov.
The electron density in the unit cell of a crystal is divided into a known and an unknown part. The structure factors of the known part are denoted by R(h). They are given by
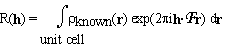. (2.1)
where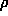 
known(r) is the electron density of the known part and 
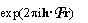is just a fancy notation for exp
.
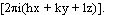Now we do something new. We make a three dimensional grid by dividing the unit cell into Pa, Pb, Pc equal parts along the crystallographic axes a, b, c respectively. The grid points are denoted by rp; p = 1, ... ,P where P = Pa . Pb . Pc. The unknown part of the electron density is described as a sum of Gaussian blobs of equal widths, centered on the grid points. Each Gaussian basis function is assumed to contain an unknown number of electrons, n(p):
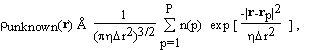(2.2)
where 
r is the mean grid spacing 
and determines the width of
the Gaussians relative to the grid spacing. If the grid spacing is
sufficiently fine, the electron density of the unknown part of the molecule can
be well approximated by such a superposition of Gaussians. When (2.2) is
extended periodically over the repetitions of the unit cell, the structure
factors of the unknown part, O(h), can be expressed as
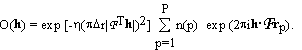. (2.3)
The notation R(h) for the structure factors of the known part and O(h) for those of the unknown part of the structure is adopted from holographic theory, where R(h) and O(h) denote the reference and object wave, respectively. The squares of the absolute magnitudes of the structure factors of the crystal, |F(h)|2, then satisfy the equations
|F(h)|2 = |R(h) + O(h)|2 = |R(h)|2 + R(h) O*(h) +R*(h) O(h) +|O(h)|2. (2.4)
As promised, the measured intensities, that are proportional to |F(h)|2, are the sum of the diffracted intensity of the known part, |R(h)|2, the diffracted intensity of the unknown part, |O(h)|2 and the interference terms, R(h) O*(h) +R*(h) O(h).
When the representation of the unknown density is substituted from (2.3), equation (2.4) becomes a set of quadratic equations in the unknowns, n(p). The number of equations, Nh, is usually not equal to the number of unknowns, P. The equations may contain inconsistent information, e.g. due to experimental errors, or lack of isomorphism in MIR, or incomplete non-crystallographic symmetry. The equations are also ill conditioned and therefore their solutions are extremely sensitive to noise in the data. Under these conditions the equations may have many solutions or no solution at all. One way mathematicians deal with these problems is by minimizing a cost function that measures the discrepancy between the two sides of (2.4). We define such a cost function as
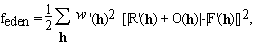(2.5)
where R'(h) and F'(h) are smeared (apodized) versions of
R(h) and F(h) and
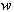'(h)2
are weights. Unless the structure factors are appropriately smeared
(apodized), the Gaussian basis functions in (2.3) are not able to fit the
experimental data. This shows up as a vicious(!) numerical instability in the
solution. Let us be even more blunt: such numerical instabilities are inherent
to inverse problems, of which the solution of crystal structures is an example;
they do not depend on the representation chosen. They cause arbitrariness in
the structures at the high resolution end of the data. In other words, no
matter how well you measure your diffraction intensities, at some resolution
your structure depends almost entirely on the structure you postulate during
refinement. We attempt to make such arbitrariness explicit and eliminate it if
possible.
The summation in the cost function (2.5) includes only available experimental data, i.e. we do not include values of R(h) for which the corresponding F(h) are missing. Thus the cost function (2.5) does not make unwarranted assumptions about unobserved reflections: their values are indeterminate, as they should be. Therefore truncation errors of Fourier inversions are absent. The solution of equation (2.5) is not unique; this is an expression of the well known crystallographic phase problem. A simple geometric representation of this lack of uniqueness is shown in Fig. 1. R(h) is the vector representing the structure factor of the known part of the electron density. The circle around the origin has the radius |F(h)|. Since the phase of |F(h)| is unknown, any O(h) that connects the tip of R(h) to any point on the circle with radius |F(h)| satisfies equation (2.4). However, additional information in the form of constraints reduces the arbitrariness of the solution. The unweighted difference Fourier solution is O2(h). If the "correct" solution is O1(h), the "dual image" is represented by O3(h).
sorry not yet available
Figure 1.
Geometric representation of equation (2.4) in the complex plane for acentric reflections.
A second type of information on the crystal structure is (possibly imperfect) knowledge of the electron density in parts of the unit cell. For example, part of the molecule may be very similar to another molecule whose structure is known. As another example, the solvent volume has a featureless electron density at a well known value. Such knowledge can be incorporated into EDEN as a "target" density, expressed in terms of the amplitudes of the basis functions used in the main program. They will be denoted by n(p)target. We introduce a corresponding cost function
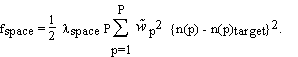(2.6)
The overall relative weight, 
space, and the individual weights at
each point,
,
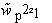express the "strength of our belief" in the correctness of the target density:
the weights may be used to emphasize or de-emphasize different regions of the
unit cell, while the overall weight determines the relative importance of
deviations in space vs. deviations in reciprocal space. In the presence of a
target density, the actual cost function used in the computer program is the
sum of feden (2.5) and fspace (2.6):
ftotal = feden + fspace. (2.7)
It can be seen from Eq. (2.3) that the structure factors of the unknown part can be calculated by fast Fourier transforms followed by a scalar multiplication. The gradients of the cost function can be calculated similarly. This leads to a fast (PlogP) algorithm and to the ability to minimize Eq. (2.7) without ever calculating or saving PxP matrices. In EDEN the cost function is minimized using a conjugate gradient algorithm that is very efficient in the presence of non linear constraints.
A basic constraint, non-negativity of the electron density, is incorporated directly into the conjugate gradient optimizer by stipulating that all elements of the solution vector, n(p), be non-negative. The constraint can be used in two different ways: in "correction mode" n(p) is bounded from below by the negative of the known initial electron density and in "completion mode" the added density itself is non-negative everywhere. Additional information leads to additional terms in the cost function (2.7).
The representation of the unknown density, presented in Eq. (2.2), uses an
overcomplete set of Gaussian basis functions that are not orthogonal to each
other. Mathematicians have done extensive research on such non-orthogonal,
redundant basis sets: they are called frames. Excellent discussions can be
found in a book by Daubechies (1992) and in a review by Heil &
Walnut (1989). Some of their important results are summarized below. The
mathematicians assure us that electron densities can be approximated well by
such representations, if the electron density does not vary too wildly.
Restated in technical language, the requirements are that the diffraction
pattern and the basis set should have similar intrinsic resolutions, and that
the grid spacing should be about twice as fine as required by the corresponding
Nyquist criterion. In our algorithm this is achieved by the appropriate
choices of 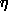and 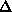r in Eq. (2.2). Although a given electron
density can be represented by several different sets of coefficients, the
algorithm used by EDEN is mathematically stable.
We tested the accuracy of our representation by placing a single Gaussian blob onto an arbitrary point on the grid and trying to represent it by our Gaussians on the grid. We found that if we use a simple grid the maximum phase error was 47o and the corresponding amplitude error was 28%. Using a body centered grid the maximum phase error was 26o and the corresponding amplitude error was 20%. The phase error for a complicated molecule that is uniformly distributed in the unit cell is expected to be less.
In our next set of tests we recovered parts of a model of Thaumatin, a protein
with 207 residues, with no noise or solvent. Without a solvent mask 70
consecutive residues could be recovered. We used the values 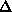r =
1.8Å and 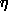= 0.28 for this test. When a hard solvent mask that
covered half the unit cell was imposed, as many as 160 consecutive residues out
of the 207 (or 77%) were found essentially perfectly. The recovered electron
density was within 10% of that of the original model and the phases were
accurate to 25o. In the next test we used 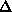r = 1.4Å
and 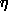= 0.75 that corresponds to an input resolution of 2.0Å. The
phase accuracy of the recovery is very good, better than 10o. The
convergence of the algorithm without a solvent mask is also better: in fact 90
out of 207 residues (i.e. 43%) were recovered essentially perfectly. With a
solvent mask or a solvent target function we got perfect recovery only up to
120 residues. This is a respectable 58%, but it is less good then using the
previous values of 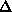r and 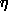. We do not understand the reasons
for the difference.
Some additional tests show the power of the positivity constraint in model
problems that have no noise or solvent. EDEN solved the model of
Staphylococcal Nuclease at 3Å resolution using a low resolution (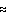
6Å) solvent target that covered 61% of the unit cell and no other
information. A similar result was reported by Bricogne (1993) using a very
sophisticated algorithm in reciprocal space. We recall that Beran &
Szoke (1995) found that the phases of the structure factors of a model
protein could be recovered completely when the electron density was given in a
little more than half the unit cell. The above results seem to contradict
recent conclusions of Millane (1996). We interpret Millane's conclusion as
establishing an upper limit to the additional information needed to solve the
crystal structure. In our opinion he does not exclude the possibility of
solving the structure with less information.
3.1. Derivation of equations for MIR. Crystal structures can be solved by multiple isomorphous replacement (MIR) if the only change in crystal structure is the addition of heavy atoms. MIR methods require that individual data sets be taken for each derivative and that the positions of the heavy atoms and their occupancies be found by Patterson or direct methods. Conventional MIR methods then proceed to find the phases of the native protein. Very often the resulting phase set does not give electron density maps that are easily interpretable. This is the stage where the holographic method can be of advantage. In principle, the holographic method is equivalent to the conventional method of finding the phases of the structure factors of the native protein. In practice, the convergence of EDEN for ab initio phasing is worse than that of traditional programs (PHASES or MLPHARE). On the other hand, we expect that a consistent use all known constraints should improve the attainable accuracy of the solution. In a test case using real data, EDEN resulted in a clear improvement over conventional methods.
From a mathematical point of view, heavy atom derivatives (as well as anomalous dispersion) increase the number of independent equations with respect to the unknowns. With a sufficient number of derivatives the phase problem should therefore be solvable. The relevant equations in EDEN are simple generalizations of (2.1) - (2.5). The unknown density (2.2) is that of the native protein. So is the structure factor, O(h), of equation (2.3). Suppose M + 1 sets of diffraction amplitudes have been measured: one for the native and one each for the M derivatives. Suppose also that the positions of the heavy atoms and their occupancies were found, using Patterson or direct methods. The calculated structure factors for the heavy atoms then belong to the known part of the structures. For the m'th derivative they will be designated Rm(h). The measured structure factors of the m'th derivative will be denoted |Fm(h)|. Then equation (2.4) can be generalized to the set
|Fm(h)|2 = |Rm(h) + O(h)|2 = |Rm(h)|2 + Rm(h) O*(h) +Rm*(h) O(h) +|O(h)|2, (3.1)
where m = 0, ... , M (m=0 designating the native protein). It can be demonstrated that, Eqs. (3.1) are equivalent to traditional MIR algorithms (the simple minded ones, see e.g. Giacovazzo 1992). Equations (3.1) are solved by minimizing a cost function that is analogous to (2.5)
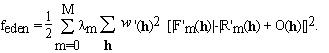. (3.2)
In equation (3.2) we introduced weights, m, that can express the
reliability or quality of the measurements of each derivative.
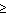0 data set can now be treated exactly as a derivative
in MIR. In P1 symmetry the h 
0 reflections are an independent
data set. The easiest way to use them in EDEN is to create a "flipped"
data set by negating all the indices of the reflections, h -> -h, at the same time flipping the signs of the phases of the heavy atoms
and declaring this new data set to be a separate derivative. Friedel's
relations apply to the structure factors of the native because that part of the
structure has no anomalous dispersion. Therefore the unknowns in this
"flipped" data set are the same as those for the h 0 data
set. In higher symmetry similar considerations apply. Equations analogous to
(3.1) are now defined and solved by minimizing the cost function that is
analogous to (3.2). It is clear that such data sets can be used together with
MIR data. The only difficulty one might encounter in this procedure is that
the anomalous data sets are weighted too heavily. The procedure is able to
solve problems in which there is no native data set, by setting o to
zero.
The EDEN implementation of the MIR algorithm suffers from convergence problems if the starting phases are too far from the correct solution. To circumvent this problem, we started from the MLPHARE estimate of the phases. The native data were placed on an absolute scale with a Wilson plot program from CCP4 using data between 3.0 Å and 1.8 Å resolution. The derivatives were scaled to the native dataset and the total number of electrons in the unit cell was estimated.
Our first step was to check the occupancies and positions of the heavy atoms. To do this, we worked at a resolution of 3.0 Å. The initial MIR phase set was used to prepare a corresponding electron density map. EDEN was run at 3.0 Å resolution in correction mode, and the resulting electron density maps were visually inspected to see if there were either peaks or holes at the heavy atom positions. Ideally, there should be no evidence of the heavy atoms in the resulting native electron density. If they do, either the occupancies of the heavy atoms or the scaling are wrong. By repeatedly running EDEN and inspecting the results we adjusted the occupancies of the heavy atoms and made slight adjustments to the relative scaling of the derivative and the native datasets.
Preliminary EDEN runs were done at 3.0 Å resolution. The results were quite encouraging. At this point the isomorphism of the derivatives was checked. In order to do that we started from the MIR map and ran it in correction mode against the measured structure factors of the native alone. This way the program is not constrained by any of the derivatives. The same procedure was done with each one of the derivatives. Pairwise comparisons of the results should reveal lack of isomorphism and local distortions around the heavy atoms. We found that, within our ability to detect differences, the two derivatives of kinesin were isomorphous with the native.
The next step was to obtain an estimate of the solvent envelope. This was done by apodizing the output of the previous 3.0Å MIR run to 7.0. The appropriate EDEN utility was used to select the 50% of the grid points with lowest electron density. These were used as the solvent region, and assigned a target electron density of 0.33 electrons/Å3.
Two EDEN runs were done at 3.0 Å resolution using the solvent
target and the two derivatives with space = 0.003 and 0.01. The
results were very encouraging, and we used the same solvent target to do a full
EDEN run at 2.0 Å resolution. The resulting electron density map
was compared with that obtained from the original phases derived from
MLPHARE, and with a DM modified map (Cowtan & Main, 1993).
The fully refined kinesin structure was used as a guide for comparing the maps.
The EDEN map was comparable to the DM map everywhere and in some
places it was clearly better.
The reader may have noticed that the kinesin work involved a large number of
preliminary runs. This is typical of the holographic method; whereas a
particular EDEN run takes only 1-3 hours on a standard workstation, many
such runs are needed to establish optimal values of critical parameters
('s, smearing factors and scaling factors). In particular, Eq. 2.4
shows that data and models must be carefully scaled in order that the cost
function minimization be meaningful.
Our approach can be described as a real space method, based on an expansion of the electron density in basis functions and on a search for the number of electrons in each one of the basis functions. It is one more step removed from reciprocal space methods then other density modification methods. Note that we almost never refer to the phases of the structure factors.
In its simplest form, the holographic method can be used to complete a partly known structure. If there are no external constraints, the electron density maps obtained using the holographic method are very similar to traditional Fo - Fc and 2Fo - Fc maps. Traditional Fourier maps are actually marginally more accurate, because the holographic method is limited in its accuracy by the (incomplete) basis function expansion. However, if there are known constraints that must be satisfied by the electron density, the holographic method is able to use that information to recover electrons more accurately than traditional Fourier methods.
The fact that the electron density is always positive is an important constraint; positivity is always enforced in EDEN. In addition, often the electron density is known in part of the unit cell, either because the solvent region is known, or because a partial structure has been placed in the unit cell. EDEN is able to use the localized nature of the known electron density in real space: it can constrain it in some part of the unit cell and not in other parts. It can also use the known electron density as a mild constraint. Therefore errors in the "known" part can be both detected and corrected.
We have shown that MIR, MAD, and NCS information can be incorporated into the holographic method. Using simulated heavy atom data, we have explored in some detail the convergence of our algorithm and the uniqueness of the solution it supplies. These simulations show that the holographic method does not converge as well as traditional reciprocal space methods, even though the equations are mathematically equivalent. However, once the electron density is within the radius of convergence of the correct minimum, the holographic method quickly and accurately finds the correct structure. Given these findings, we propose that conventional methods should be used to identify an initial MIR solution, and that the holographic method should then be able to improve that solution. We have made use of this strategy to determine the structure of the protein kinesin, using experimental MIR data. An initial structure of kinesin was identified using the program MLPHARE. Using EDEN to optimize this solution led to a clear improvement in the resulting electron density maps.
On the theoretical side, we scrupulously differentiate between lack of information and tacitly assumed information. For example we consistently avoid the use of Fourier back transforms. In usual practice, unknown structure factors are given zero value as opposed to keeping them unknown. Similarly, in the presence of non crystallographic symmetry, some formulations implicitly assume that the electron density is featureless outside the symmetry related regions. We try to live by L‡nczos' dictum: use all the available information and no more. In principle, given a sufficient amount of information it is possible to recover the crystal perfectly. However, different algorithms may have very different convergence properties and may have very different sensitivity to imperfections in the data. In our opinion, this last point alone is sufficiently important to justify the development of new methods for crystallographic computations.
Finally, we want to give a preview of coming attractions. In the near future
we intend to extend the variety of real space target functions. We will then
be able to treat molecular replacement and resolution extension (usually called
phase extension) conveniently. Following David & Subbiah (1994), we will
also try to solve proteins ab initio at low resolution using our algorithm. We
have already found that the holographic method converges well in the presence
of low resolution information. At high resolution we will incorporate
atomicity, i.e. our own version of Sayre's equation. Both the low resolution
and the high resolution information can be cast in a very transparent and clean
form. In reciprocal space, we will use 1/
2 weights for the
measured structure factors, in order to take into account inaccuracies of
measurements. We will also incorporate some statistical information: The
probability distribution of the measured structure factors can be estimated
more accurately than given by the single number 2.
Similarly, the probability distribution of the unmeasured structure factors can
be estimated. If the number of missing atoms is known, the probability
distribution of the missing part O(h) can be estimated. The most
exciting (and difficult) development is the incorporation of some chemical
knowledge into the holographic method. It has the following ingredients:
Kleywegt has shown how to fit small parts of proteins into the electron
density. We intend to use a variant of his method. Also Fortier has shown how
to find extremal points of the electron density and how to connect them to find
the protein backbone. We also intend to use a variant of her method. Finally,
we intend to put in a mock-electrostatic force in order to improve the electron
density and to impose chemical constraints on it. We hope that our efforts
will be a beginning of "automated" crystallographic refinement.
Beran, P. & Szoke, A. (1995). Acta Cryst. A.51, 20-27.
Bricogne, G. (1993). Acta Cryst. D49, 37-60.
Bricogne, G. (1992). International Tables for Crystallography. Vol. B. edited by U. Shmueli. Dordrecht: Kluwer Academic Publishers.
Cowtan, K. D. & Main, P. (1993). Acta Cryst. D49, 148-157.
Daubechies, I. (1992). Ten Lectures on Wavelets. Philadelphia, PA: SIAM.
David, P. R. & Subbiah, S. (1994). Acta Cryst. D50, 132-138.
Giacovazzo, C. (1992). editor, Fundamentals of Crystallography. Oxford: IUCr, Oxford University Press.
Heil, C. E. & Walnut, D. F. (1989). SIAM Review 31, 628-666.
Kull, F. J., Sablin, E. P., Lau, R., Fletterick, R. J. & Vale, R. D. (1996). Nature 380, 550-555.
L‡nczos, C. (1961). Linear Differential Operators. London: Van Nostrand.
Maalouf, G. J., Hoch, J. C., Stern, A. S., Szške, H. & Szške, A. (1993). Acta Cryst. A49, 866-871.
Millane, R. P. (1996). J. Opt. Soc. Am. A13, 725-734.
Somoza, J. R., Szoke, H., Goodman, D. M., BŽran, P., Truckses, D., Kim, S-H. & Szoke, A. (1995). Acta Cryst. A.51, 691-708.
Szoke, A. (1993). Acta Cryst. A49, 853-866.
Szoke, A., Szoke, H. & Somoza, J. R. (1997). Acta Cryst. A.53, To be published.